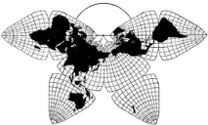
Cahill 1909
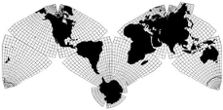
Cahill-Keyes 1975

Cahill 1909
|
Go back to
Gene Keyes home page
Cahill-Keyes 1975 |
|
Why Cahill? What about Buckminster Fuller?
Evolution of the Dymaxion Map: An Illustrated Tour and Critique Part 9.6 by Gene Keyes 2009-06-15 CONTENTS
Click inside boxes to open other sections in separate windows. 9) Critique: Seven Design Flaws of Fuller's
Map as Compared to Cahill's
|
|
Part 9.6
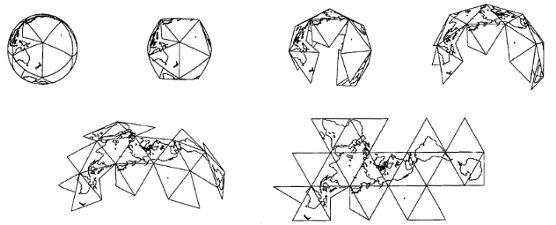
Poor to zero comparison with any equivalent globe Fig. 9.6.1 below: Despite the drawing below,
and the nifty animation
already shown in Part 7, a Dymaxion map does not have a cognate globe
with which it can be compared.
|
Source: verso text of smaller ODT Raleigh map, 2009 Scanned by Gene Keyes |
|
Fig. 9.6.2 below: One of the buzzwords in
Fuller's lexicon is "modelability". But it is Cahill, not Fuller,
who models the globe to perfection with his map, and vice
versa. A Cahill map is the alter ego of a globe.
|

Source: 1919 brochure by Cahill; scanned by Gene
Keyes
|
|
Fuller's map, on the other hand, is a sophisticated
geodesic abstraction. It is not a hands-on model that any pupil
can use for immediate and comprehensible comparison to a globe.
(Nor to an atlas.) Yes, there is that graphic animation of
globe to icosahedron to map, but it is a quick and passive piece
of digital legerdemaine. Yes, there is a fold-up icosahedron; but
it is a flat-faceted novelty, not a globe. These badly lack what I
describe later in Parts 9.7-a and 9.7-b, a synoptic view of globe
and map together.
Instead, what we see in the Dymaxion sketch above, is a partial view of a globe, minus its graticule; then a partial sketch of an icosahedron, minus its graticule; then the map unfolding to its flat form, minus its graticule. Indeed, there is no actual spherical-icosahedral globe a la Fuller at all (except for one I improvised, shown in Part 9.7-a, where I will further discuss and illustrate the Dymaxion map's poor fidelity to a globe.) |
|
But meanwhile, let us return to the 5°,
50-inch "President's Globe" for FDR and Churchill, depicted in
Part 2. I first saw it in the March 1, 1943 Life, then I saw
it in real life at the Library of Congress in Washington, DC. Why should
that be the only earth-sphere with a 5° graticule? Why not every
globe of any size? (Most globes have 15° graticules; a
few have 10°.)
Below I will show four big pictures of the FDR globe, plus three of the same pictures enhanced as if with Cahill-type octants. The point of this next set of images is to underscore that for purposes of comparison, a globe and a world map should have a 5º grid. Until the Internet, these President's Globe images were as rare and almost impossible to find as a 5º globe itself. My educational purpose here is no secret: a 5º globe next to any 5º world map — except Cahill — will show up all other world maps for their distortions: and that goes for Fuller as well. The Dymaxion map's failure to show a 5º grid is a major indicator of its lack of fidelity to a globe. (And if it did have 5º, so much the worse, as we saw in my Grip-Kitrick examples in Part 9..2.) On the other hand, a 5º Cahill world map, plus a 5º globe, are the foundation for an accurate and proportional concept of the Earth. |
|
Fig. 9.6.3 below: There is, or was, perhaps,
another 5° globe, desk size, not floor size: seen in a photograph of
prominent cartographer Arthur H. Robinson (1915-2004), none other than the
producer of the President's Globe. If my astigmatic eyes do not deceive
me, I believe that in this picture of Robinson, his globe has a 5°
graticule. Was it a working model for the 50-inch goliath? Or a small replica?
(Image shown here at double its Internet original.)
|
| For a smaller size of this
picture, click in it once; to restore enlarged size, click in it twice. 
|
| Fig. 9.6.4 below: FDR himself
looking at the giant 50-inch globe, which is on floor beside his
desk. Again, I have doubled the Internet original of this picture. |
| For a smaller size of this
picture, click in it once; to restore enlarged size, click in it twice. 
Source: Library of Congress: http://www.loc.gov/exhibits/churchill/interactive/_html/_items/wc0001_3.jpg |
|
Fig. 9.6.5 below: President's Globe in
FDR's office. One of those full-size Life photos from the Google-Life
archive.
|
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.

Source: http://tbn0.google.com/hosted/images/c?q=9cace840c302e172_large |
|
Fig. 9.6.6 below: Now, imagine any size
of 5° globe enhanced at the octant division lines a la Cahill.
This is Fig. 9.6.5, as changed by me:
|
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.

Source: http://tbn0.google.com/hosted/images/c?q=9cace840c302e172_large Cropped at top and bottom, and octant division lines added by Gene Keyes. |
| 9.6.7 below: Another closeup
of the President's Globe; repeated here from Part 2. |
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.

Source: Google Images Life Magazine archive: http://images.google.com/hosted/life Via this search: roosevelt globe (otherwise hard to find) http://tbn0.google.com/hosted/images/c?q=764046a9c4937dfd_large Date taken, 1943; photographer, Thomas D. Mcavoy Original caption: "View of globe in President Franklin D. Roosevelt's office." |
|
Fig. 9.6.8 below: Another octant-enhanced
view of the President's Globe, as changed from Fig. 9.6.7 above.
|
|
For a smaller picture size, click in it
once; to restore full size, click in it twice.

Source: http://tbn0.google.com/hosted/images/c?q=764046a9c4937dfd_large Other source details at Fig. 9.6.7, ibid Octant lines added by Gene Keyes. |
|
Fig. 9.6.9 below: President's Globe, in
color; I have doubled the Internet original of this picture.
|
| For a smaller size of this
picture, click in it once; to restore enlarged size, click in it twice. 
Source: http://www.loc.gov/exhibits/churchill/interactive/_html/_items/wc0001.jpg |
| Fig. 9.6.10 below: One
more enhanced President's Globe, from Fig. 9.6.9. |
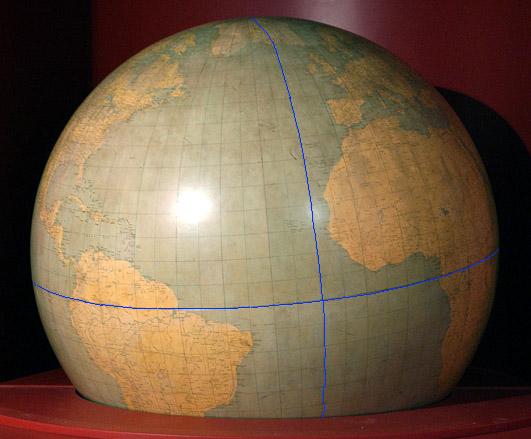
Source: http://www.loc.gov/exhibits/churchill/interactive/_html/_items/wc0001.jpg Octant lines added by Gene Keyes. |
|
Fig. 9.6.11 below: Back in 1976, I had
already done a similar octant enhancement with my ten-inch Replogle globe.
Like most, this one has a faint 15° graticule. I applied a Letraset black
line to highlight the Cahill octants; relatively easy. For the next 33 years,
I wished it had a 5º graticule, but didn’t want to go to the bother
again, as I had in 1974, of drawing 5° on a 12-inch globe for an icosahedral
net. (See Part 9.7-a.)
|

Source: Photo by Gene Keyes, 2009
|
|
Fig. 9.6.12 below: Then, for the sake of
this website, I gritted my teeth and penciled in an improvisational
5° grid. It only took me five days. (Don't worry; I have a life,
and can afford the time, being retired. ;-)
In a real, commercially-produced version, the 5º lines would be more precise and not as thick. |

Source: Photo by Gene Keyes, 2009
|
|
Appendix: Behind the Scenes of that 5º
Penciled Globe
|
|
Fig. 9.6.13 below: Perhaps I should scrounge
up a bunch of money, and commission a professionally drafted 5º
globe with Cahill-Keyes octants; or else should have printed out some 5º
globe-map gores and pasted them onto a sphere. (And I'd still prefer 1º
as well, but that's quite a job . . .) Meanwhile, to demonstrate the principle
in a dummy format, I used an existing 1975 Replogle globe. Its surface
is very slick, and difficult to write on; I couldn't dare use a pen
or marker (except for the Cahill lines), so pencil it was. The globe's
semi-circular holder was unsuitable as a drawing aid, therefore, to
do the meridians, I used a flexible curve (spline), which had to be affixed
to the globe with a piece of sewing elastic, clamped to the spline. (Below.)
I had made tics with a (costly!) ten-point divider to split the 15º
meridians into three. Doing the parallels was even more difficult; closer
to the poles, I could use a compass. Then, remounting the globe in a
different spindle, I was unable to clamp the pencil firmly enough to
the outer rim, and eventually had to get Mary Jo to hold the pencil
against the rim, while I oscillated the globe back and forth enough times
for the line to show up.
|

Source: Photo by Mary Jo Graça, 2009
|
|
As mentioned, in 1974 I had drawn a similar 5º
grid on a different globe and enhanced it with map pins and yarn to replicate
a Dymaxion spherical icosahedron. This endeavor, illustrated in the
next part, was yet another confirmation to me that the Fuller map was
not a good teaching and learning tool.
|