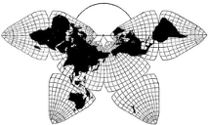
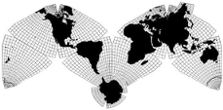
Cahill 1909
| Go
to Gene Keyes home page |
|
| Go to complete linklist of Cahill-Keyes
map development |
|

|
 |
|
Cahill 1909
|
Cahill-Keyes 1975 |
|
Gene Keyes
B.J.S. Cahill's World Map Variants:2016-09-06 1) Conformal |
|
In the 30 years after Cahill published
his initial
Butterfly map in 1909, he also produced several
"Variants" as well as other false starts, with a confusing
array of nomenclature and neologisms. However, besides the
1909 original, Cahill settled on three main types, the
clearest illustration of which is in this [1934] offprint
from Nelson's Encyclopedia:
1) Conformal
2) Equal Area 3) Gnomonic |
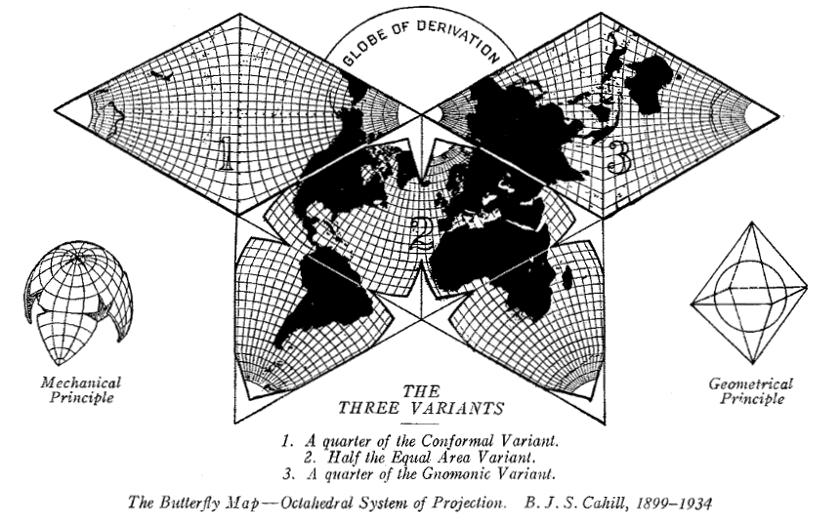 Source: B.J.S. Cahill, "Projection"(Nelson's
Encyclopedia, [1934], offprint;
also in Cahill, "The Butterfly Map: Octahedral System of Projection" (Pacific Marine Review, 1938-09) p. 42-43. Scanned and enlarged by GK from a duplicate offprint received from B.J.S. Cahill Collection at The Bancroft Library, University of California, Berkeley. Note: on an earlier page, I showed a smaller enlargement of this image at the same scale of 1/200 M as a set of other Butterfly maps. Here, I have made it yet larger for emphasis of the Three Variants. |
|
A conformal map is one in
which meridians and parallels cross one another at right
angles — as on a globe, but much more problematic when it
comes to devising a flat world map.
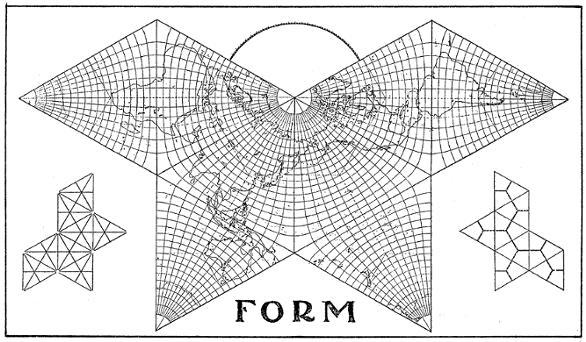
On Cahill's earliest map, the graticule was a very well-drafted custom-made assembly — he was an architect, remember —, but it was derided by ultra-mathematical cartographers. So Cahill set about making some more rigorously mathematical variants, and even hired the prominent mathematician Oscar S. Adams to compute their graticular distributions at five-degree intervals for all three main variants. Meanwhile, Cahill had not forgotten what I consider his foremost principle: The creation of a master plan of the world is a matter of design first and foremost, the design of a frame within which intensive mathematical details shall be afterwards subordinated. (1928)In most of his examples, Cahilll's Conformal is embedded in equilateral triangles, unlike the truncated ones of Variant 2, the Equal Area (and the curvilinear octants of his 1909 original). Below is an undated [mid 1920s?] Cahill Conformal draft in the North Pacific Butterfly orientation, one of a number of illustrations ["Fig. 5"] for an unpublished article or book manuscript. Like his earlier maps, it has his dubious 7.5 x 10º graticule, which conceals the split geocells along the perimeter meridian. (By 1927, Cahill was at last showing a 5º graticule.) Source: B.J.S. Cahill Collection at The
Bancroft Library,
University of California, Berkeley; Xeroxed, then scanned and reduced to 98% of original for a scale of 1/200 M by GK. |
|
|
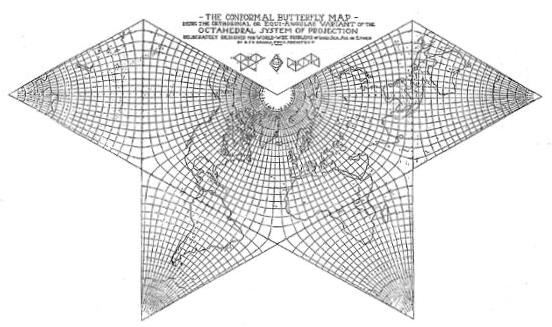
The next one [mid 1920s?] is done at 5º
resolution, betraying the sore-thumb two-and-a-half-degree
geocells along the outer perimeter. (In this version,
however, Cahill has omitted the internal northern triangle
sides, concealing the half-degree problem.in those areas.)
Source: B.J.S. Cahill Collection at The
Bancroft Library,
University of California, Berkeley; Xeroxed, then scanned and reduced to 75% of original for a scale of 1/200 M by GK. (Larger copies further below.) |
|
|
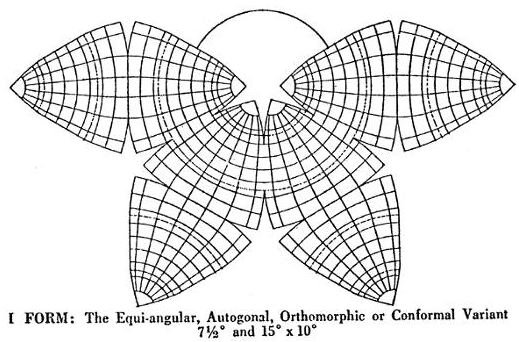
This 1924 drawing is perhaps the only
instance in which Cahill showed a Conformal graticule
inside curvilinear octants, whereas his other Conformals
were all done with equilateral triangles. So far as I
know, he did not develop this version, nor add the
continents, etc., unlike the triangulars. Here we see his
excess nomenclature: three other titles (unused) besides
Conformal.
Source: excerpt from a 36 x 57 cm (14 x
22") broadsheet. "The Butterfly Map"
at The Bancroft Library, University of California, Berkeley; Xeroxed and spliced, then scanned and enlarged to 175% for a scale of 1/200 M by GK. |
 |
|
As I've mentioned elsewhere, Cahill
seemed to "steal" my ideas before I was born, including
the "M" layout instead of his predominant Butterfly. Below
is an unpublished Cahill draft, n.d., ca. 1927, of the
Conformal variant in an "M" shape. I do not know the
purpose of the internal scaffold lines, but the four
diagonals across the triangles' altitudes once again show
what I regard as his design mistake of dividing the
meridian-perimeter geocells in half, e.g., at 22.5º W
instead of 20º as I did (and Steve Waterman
independently). Using 20º, the altitude of each octant
would be a central meridian 45º from either edge, instead
of a column of bisected geocells. But at least this draft
has the far preferable 5º geocells.
Source: Xerox from Cahill collection at
The Bancroft Library,
University of California, Berkeley; scanned, spliced, and cleaned by GK. |
 |
|
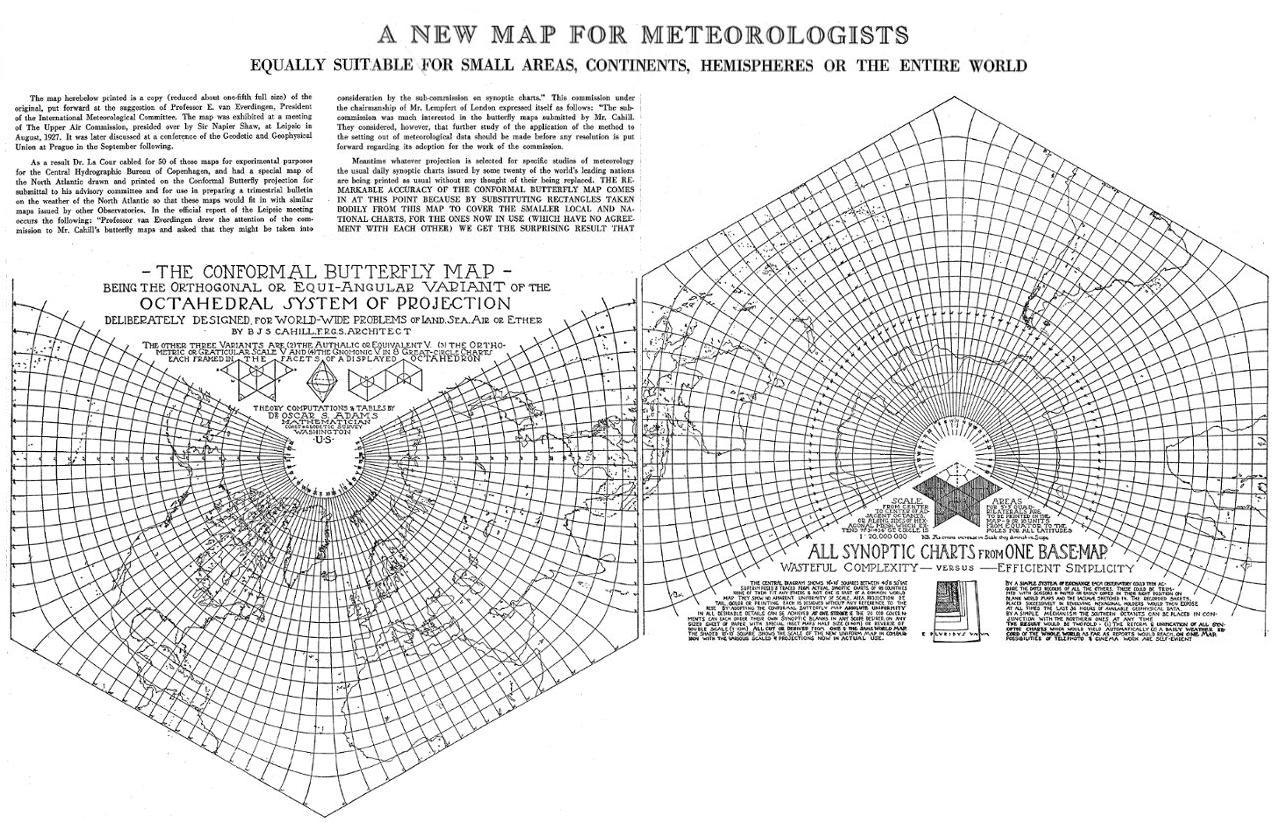
The next item [1928] is similar to
Cahill's double piece* in the April 1929 Monthly
Weather Review, but not entirely.
It is a broadsheet, 30 x 47 cm (12 x 18.5"), packed with tiny print because it was reduced from an original five times larger. [I have a complete scan of the small one, shown here, but only a Xerox-splice portion at the original size.]. So I re-enlarged the reduced typeface in separate frames below, to make its important content legible, especially the lower right section, "All Synoptic Charts from One Base Map", where Cahill again voices themes that I was discussing 45 years later, before I found he too had raised many of the same concerns. The map itself is in still another layout, a North and South zigzag spread, which Cahill thought might be apropos for a consolidated world weather map. Source: item #23 in The Bancroft Library Cahill Collection, as scanned in several parts from original and spliced by GK in ClarisWorks Draw. Note: whereas this map was split
over two non-adjoining pages in the Monthly
Weather Review, there was a single-page version in the 1934 "A
World Map to End World Maps" article, but with
different captions and 23 overlapping frames from
various weather stations. Link is to image as
scanned, rotated to horizontal, and enlarged by GK.
The text from this broadsheet image will be
enlarged in the subsequent figures.
|
 |
|
Above is the map's broadsheet
which I scanned and uploaded at its actual 1/5 size
version.. In the next frame are detail-enlargements of its
text portions. In the first subtitle cut below, we again
see Cahill's confusing nomenclature: unillustrated mention
of his otherwise unused terms "Authalic", "Orthometric".
and "Graticular Scale". (I was also confused at first by
the character "V", thinking it was a Roman numeral for "5"
among Cahill's versions; but it is an abbreviation for
Variant.) Note also the credit to Dr. Oscar S. Adams, the
prominent mathematician whom Cahill hired to calculate all
three Variants subsequent to the original.
|
 |
| Below are more of the
enlarged text details from the same broadsheet by Cahill;
source as noted above. —GK |
      
|

|
| Why am I
focusing on the Conformal, when I like his original and the
(inwardly-truncated) Equal-Area Variants better? For several
reasons, shown separately below. (a) Apart from a big
hand-colored wall-size draft of the Original, the
Conformal was his most developed and even had a printed
partial one-degree version of the North Atlantic (next image
below); (b) In 1937, the International Meteorological
Committee came within one vote of adopting the Cahill
Conformal for world weather charting, on a single base map
in place of five different ones being used; (c) In early
1975, when I was looking for a Cahill print to work on, (and
thereby supplant my earlier use of Fuller's icosahedral),
the 5º version in the Monthly Weather Review was the
only practicable one then available to me; (d) But I didn't
like the full-triangle version because one could not show
complete polar areas, and I soon moved on to my own Cahill
re-design, with a proportional geocell graticule. (e) Then, in 2015, Jacob Rus began developing a Cahill-Keyes-style Conformal version within truncated triangles having 90º right-angle apexes. He has delved much more deeply into the math of the Conformal than I could or would. The results are promising so far, and shown at the end of this page. |
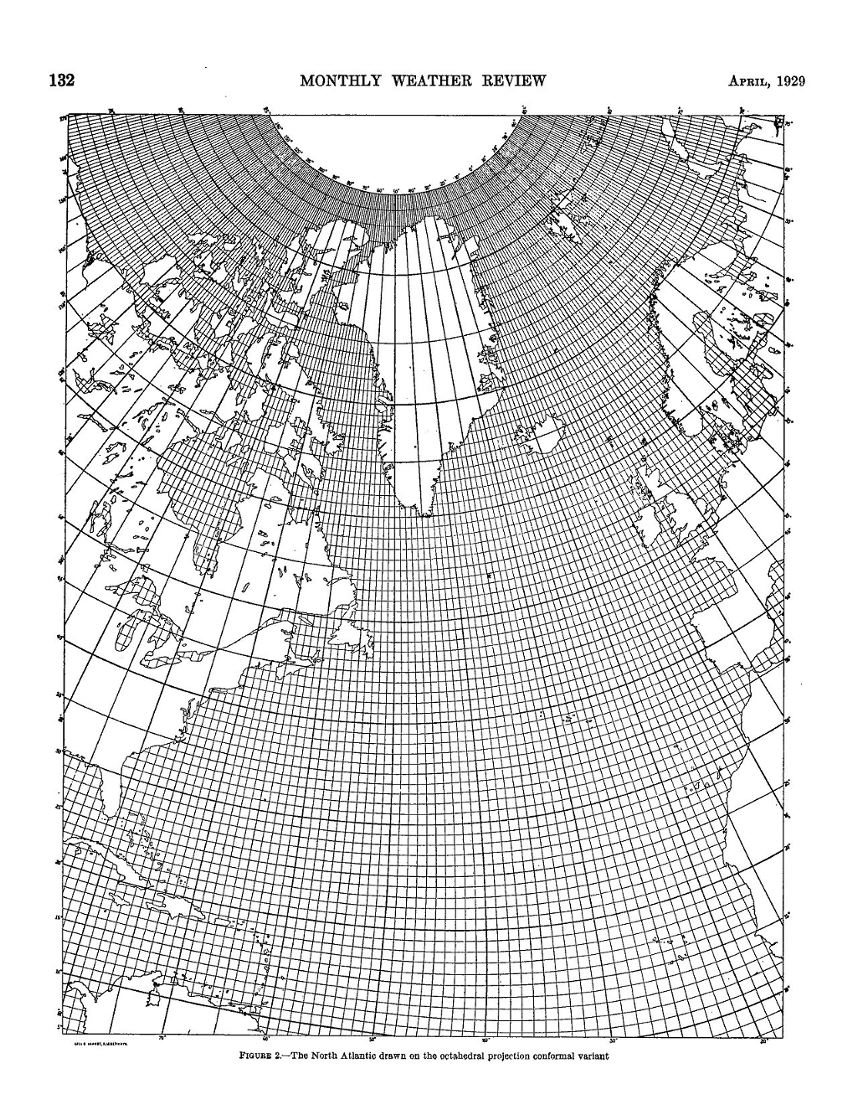
| So here is
the one-degree excerpt — but only an excerpt, because from
what I saw at the B.J.S. Cahill collection at UC Berkeley,
there was not an entire world map made at this resolution:
only the better part of the northern and southern
hemispheres on two sheets. A nice piece of work, and I
wished the one-degree cells also covered land areas. Upon
later examination, I saw that the northern latitude heights
were larger than temperate ones: shades of Mercator, and
there goes Greenland again: another reason why I strove to
make my own Cahill, without great geocell disparities. Jacob
Rus avoided the same pitfall. Like Cahill's five-degree version in the broadsheet, this too was 1/20,000,000 in the original. (See next image after this.) |
 |
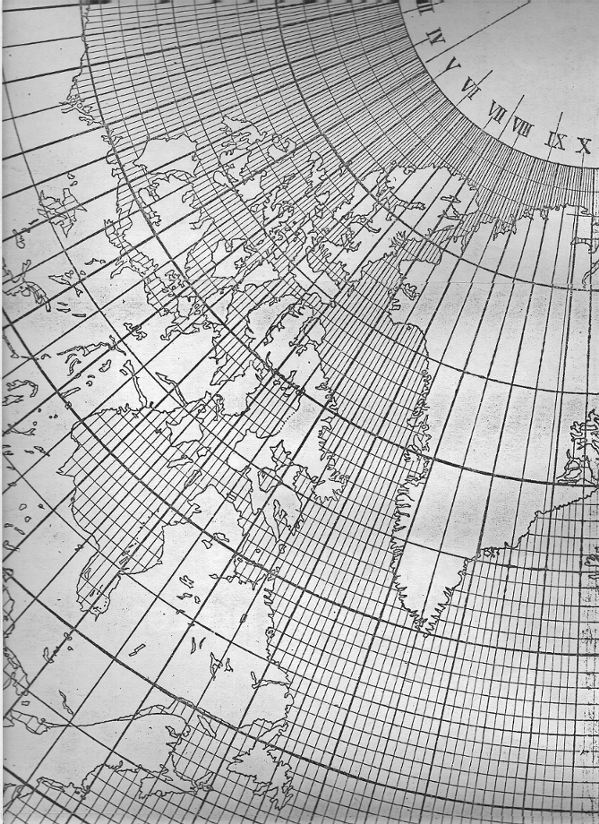
| While at
the Bancroft Library in 1983, I xeroxed a full-size 1/20,000
version, in many pieces, and later spliced them together as
best I could. As mentioned, the map was not complete, but
had significant portions of the northern and southern
hemisphere on two sheets, and was dated Feb. 19, 1929. This
is what a portion looks like.
Source: The Bancroft Library Cahill Collection.
(Listing items 19 and 20.)
|
 |
|
Some Early Starts and Work in Progress based on
the Conformal |
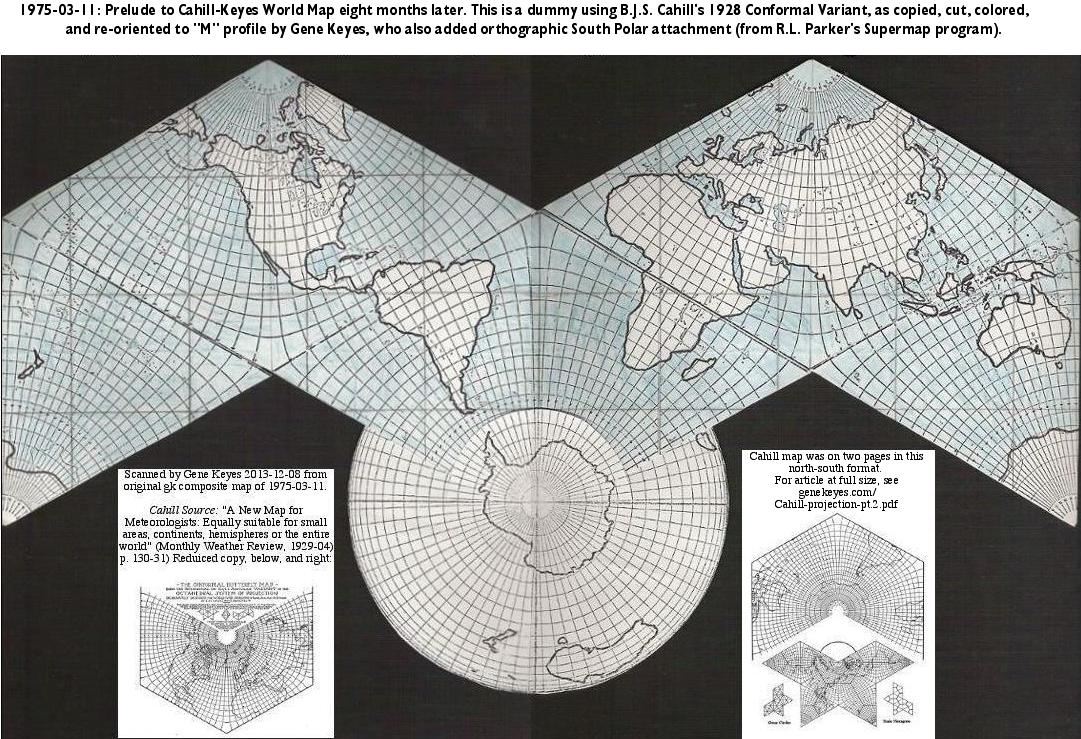
| In March
1975, eight years before I saw the one-degree Conformal, I
began my effort to make a revised
standard Cahill in the M-profile, by xeroxing the Monthly
Weather Review illustrations, cutting their
triangles out and re-configuring them. Then I enhanced the
coastlines, added blue coloring, and spliced in an
orthographic version of Antarctica, because the triangular
Conformal could not piece together the frozen continent.
(Note that I also drew in the missing triangle sides.) This preliminary dummy, at 1/100 M, was a huge step forward for me, but already the shortcomings of the triangular Cahill Conformal were becoming apparent: the Antarctica problem, the half-geocell problem, and the uneven distribution of parallels, resulting in polar regions that were swollen as well as incomplete. Whereupon, in November 1975 I drafted the first Cahill-Keyes with its proportional geocell graticule; coincidentally at the scale of 1/20 M used by Cahill to exhibit his Conformal. (My wall map dummy was at five degrees, to which I laboriously filled in one degree geocells by hand.) |
 |
| I had
thought the Conformal was unsuitable for a Cahill-Keyes
master map, until 30 years later in 2015, when Jacob Rus
sent me his aforementioned Conformal draft of Cahill-Keyes
in truncated octants, enabling the reassembly of Antarctica,
and an overall world map essentially similar to mine, but
with better underlying math. Below is is a screen grab, reduced to 10%, of a joint pdf of the Cahill-Keyes Beta 2 Megamap, and just below it, is a very early draft, 2015-04, of the Cahill-Keyes in a Conformal rendition by Jacob Rus, also at 1/1,000,000, set in the same grid as mine of 40,000 mm width. To see the full-size very sharp original pdf, download the combined pair here* and follow my instructions for easily viewing the humongous images, in the Foxit reader (now available for Windows, Mac, and Linux). *Note: you should "save link as", and then open it with the Foxit pdf reader. Suffice to say that my graticule is sui generis with proportional geocells, and that the Rus Conformal's math is over my head. But at minimum his produces better curves, and truly right-angle geocells, besides keeping my proportionality precept. (And Rus made the joint pdf, at a file size of only 18 MB, almost half of my single original.) |
|
[This one: the Gene Keyes Beta 2 version.] [Below: the Jacob Rus Conformal version] |
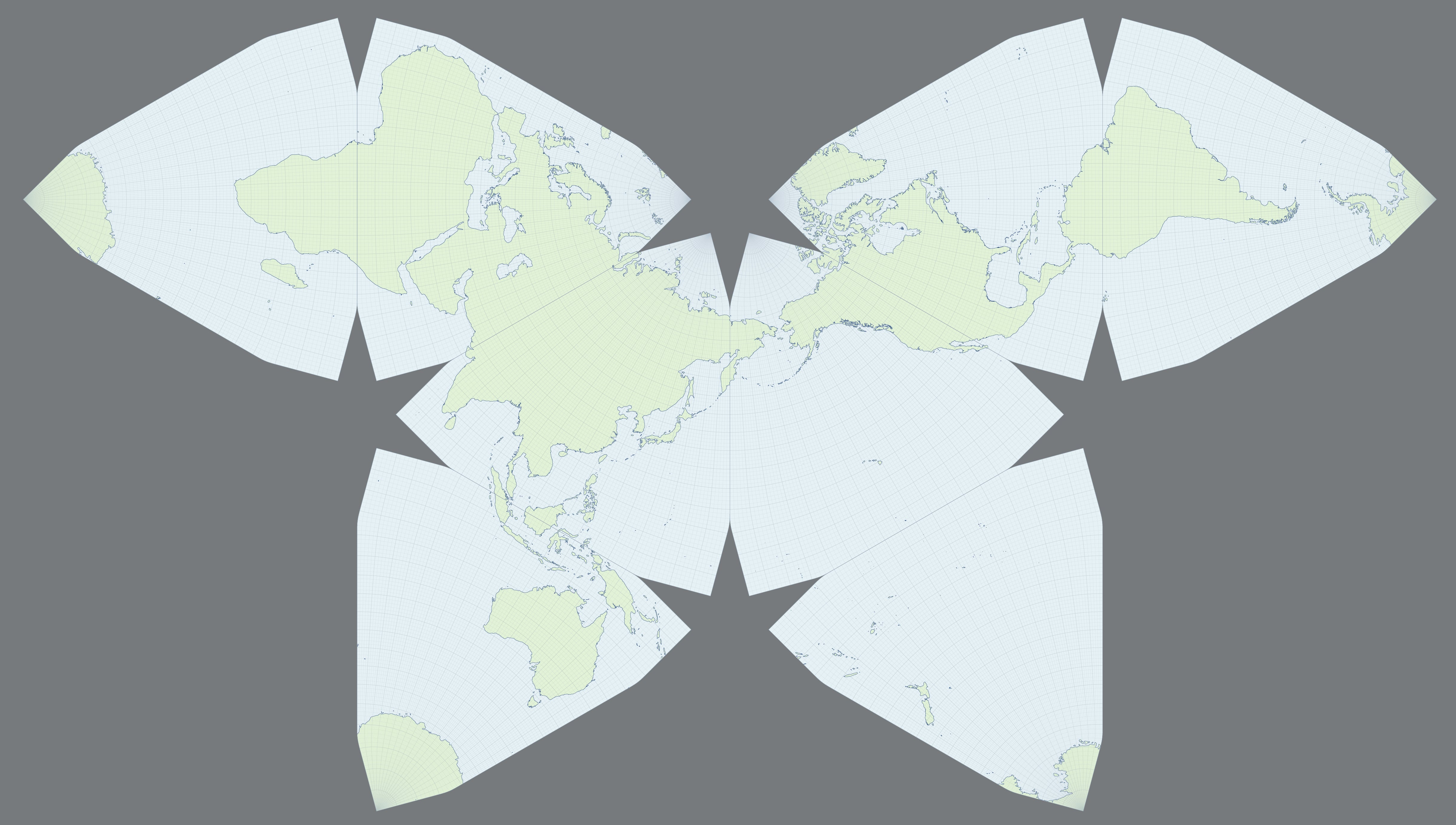
| Next is an
early draft of a Jacob Rus Conformal a la Cahill-Keyes
precepts, but without my grid overlay, and in a Butterfly
profile. (And lacking an assembled Antarctica.) This too is
a reduced version of a big image; the original jpeg is five
times larger. Click on it once for full size, to reveal the
one-degree graticule, hallmark of the Cahill-Keyes endeavor;
reload to restore the small size. Thus, another step in the slow saga of Cahill development. As the Danish poet Piet Hein put it, TTT: Things Take Time. |
To view at full size,
click image once. To restore small size, reload.
 |