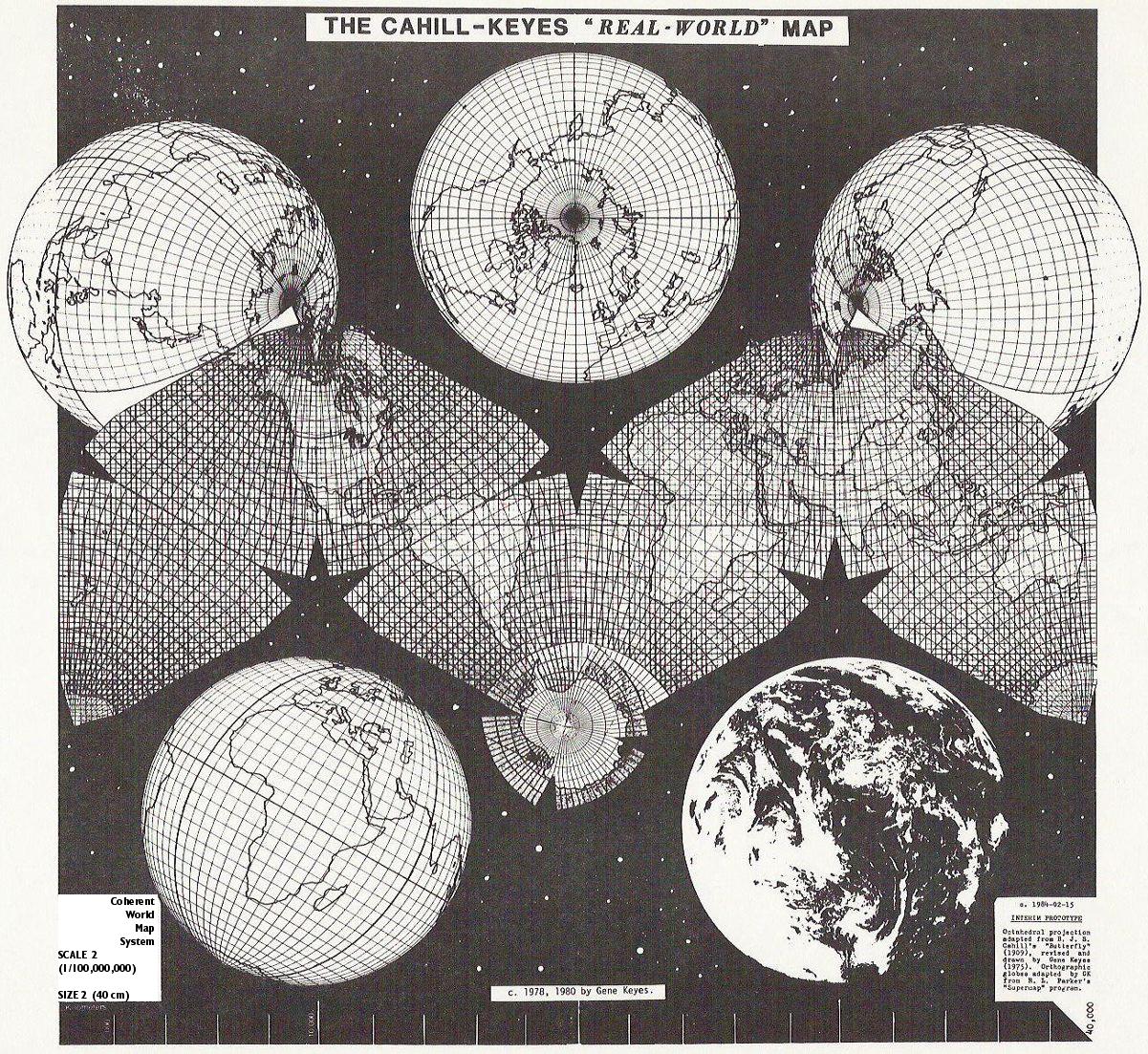
c. 1975, 1980, 2006, 2009 by Gene Keyes.
(But I'm not a big stickler on intellectual property rights.)
;-)

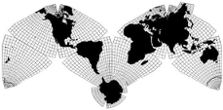
This and the smaller version on my home page are replicas of an existing 1/20,000,000 "Jr. Master" wall map 2 meters wide, and an exact floor plan of a proposed 1/1,000,000 "Mega-map" with sides 40 meters or 132' wide.

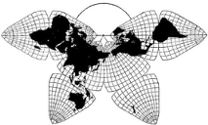
This map is adapted from the B.J.S. Cahill octahedral "Butterfly" projection, published in 1909. The graticule was newly devised, computed, and drawn by Gene Keyes in 1975, along with the coastlines, boundaries, and overall map design.

Scale adjustment for varying computer screens:

Your mileage may vary! Monitor size and settings make a difference. If the distance between the outer tics is 400 mm, then the map depicted is 1/100 million, as in its "original". In any event, the span shown is 40,000 km, representing the unfurled circumference of the earth.

This HTML web page and map jpeg were originally produced on a Mac G3 and a 19" LCD monitor with a resolution of 1024 x 768, + 75 hz. If you want the real scale as seen on your screen, measure the distance in millimeters (which is variable) between the first 2 numbered tics, then divide that into the kilometer distance (which is constant) at the middle tic, and add the term "million".* For example, on my 17" monitor hooked to a Linux Asus eee 701 with the same resolution, the midpoint distance is 178 mm, not 200, as in my "original". Dividing 178 into 20,000 indicates that on that monitor the scale is 1/112 million, not 1/100 million. See also my "Notes on Scaling Cahill and Cahill-Keyes Maps".

* The above division is a shortcut, to avoid entering a lot of zeroes in a calculator, and we take a readout of, say, 112.3.... as the fraction 1/112 million.

Metrically, the earth's circumference is approximately 40,000 kilometers, or 40,000,000,000 millimeters (forty billion), there being 1,000 millimeters in a meter, 1,000 meters in a kilometer, and 1,000,000 millimeters in a kilometer.

So if we have a [Cahill-Keyes] world map that is 400 millimeters long, equatorially, and the equator being 40,000,000,000 millimeters around, we make a fraction of

400 mm                   
40,000,000,000 mm

knock off a couple of zeros:

4 mm                   
400,000,000 mm

reduce:

1 mm                   
100,000,000 mm
 
and get the scale of 1/100,000,000. (Representative Fraction.)

Which is also to say:

Each millimeter on the map represents 100,000,000 millimeters on the ground.

Or, knocking off six zeroes to convert to kilometers, 100, we say that each millimeter on this map represents 100 kilometers on the ground.

Or, if your computer has made this map somewhat smaller than the original, as in my example above, then each millimeter represents 112 kilometers, not 100.