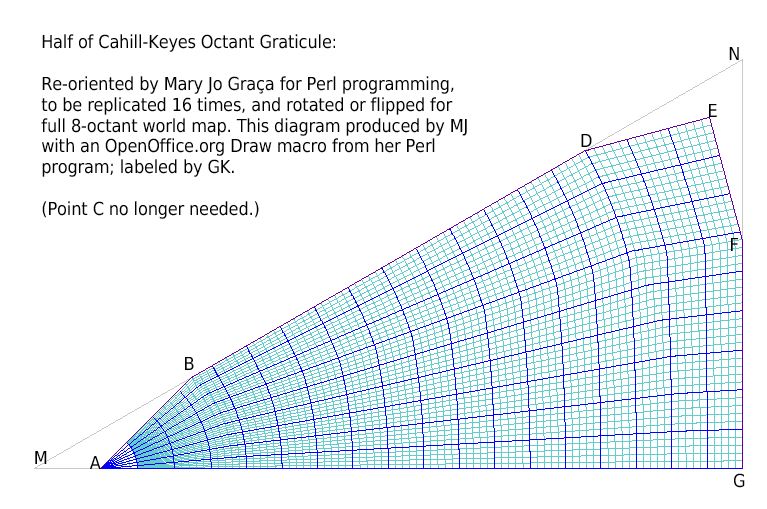
#! /usr/bin/perl -w
# Program HalfOctant8. Modified from program HalfOctant7 on 2010-04-18.
# Program outputs all the coordinates as a text file with tab separated values
# (csv format) which can be read by a spreadsheet program such as Excel or
# OpenOffice.org.
#
# Parts relating to TurboCAD macros, including functions for coordinate conversion,
# were deleted on 2010-08-05, since we've given up on using our old version of TurboCAD.
#
# Parallels in this version are as follows:
# - Latitude 75° to 89° — parallels are circular arcs with center at point A; parallel spacing is
# 104.
# - Latitude 74° — circular arc, with center at A and radius 100 more than parallel 75°, from
# meridian 0° to meridian 30°; half way between parallels 73° and 75° from
# meridians 31° to 45°.
# - Latitude 73° — circular arc, with center at A and radius 100 more than parallel 74°, from
# meridian 0° to meridian 30°; straight line from meridian 30° to meridian 45°,
# perpendicular to line BD.
# - Latitudes 1° to 72°, meridians 0° to 29° — equally spaced along meridian from equator to
# 73° of latitude.
# - Latitude 15°, meridian 45° — at the tropic joint, that is, at point D.
# - Latitude 15°, meridians 29° to 45° — circular arc; center chosen on the extension of line
# M-B-D-N, the side of the octant (corresponding to meridian 45°). Center is
# determined by: drawing chord from meridian 29° to 45°; drawing a line
# perpendicular to this chord, through its mid-point; finding intersection with
# line through point M (0,0) with angle of 30° (that is, with line M-B-D-N).
# - Latitudes 1° to 14°, meridians 30° to 45° — equally spaced along meridian, from equator
# to parallel 15°.
# - Latitudes 16° to 72°, meridians 30° to 45° — equally spaced along meridian, from parallel
# 15° to parallel 73°.
#
# Multidimensional arrays are done with hashes, with the keys used for i,j indexes.
use Math::Trig; # Call for library of trigonometric functions
# Given input
$xM = 0; $yM = 0; # Point M is the origin of the axes
$MA = 940; # Indent of octant's apex, with respect to triangle's
$xG = 10000; $yG = 0; # Point G, at center of base of octant
$DeltaFrigid = 104; # Distance for each degree of latitude close to the pole
# Other points and lengths of special interest
$xA = $MA; $yA = 0; # Point A, at the indent
$xN = $xG; $yN = $xG * tan (deg2rad(30)); # Point N
($flag, $xB, $yB) = LineIntersection ($xM,$yM,30,$xA,$yA,45); # Point B
if ($flag ne "Intersect") { die "$flag while calculating point B.\n"; }
$AG = $xG - $xA;
$AB = Length ($xA, $yA, $xB, $yB);
$EF = $AB; # Sometimes I prefer AB, others EF
$MB = Length ($xM, $yM, $xB, $yB);
$MN = Length ($xM, $yM, $xN, $yN);
$xD = Interpolate ($MB, $MN, $xN, $yM); # D is away from N as B is away from M
$yD = Interpolate ($MB, $MN, $yN, $yM);
$xF = $xG;
$yF = $yN - $MB;
$xE = $xN - $MA * sin (deg2rad(30));
$yE = $yN - $MA * cos (deg2rad(30));
$FG = $yF;
$BD = Length ($xB, $yB, $xD, $yD);
$EFG = $EF + $FG;
# Calculate polar start, two joints, and equatorial end, for each meridian; hashes %xJ, %yJ.
# Also calculate a few other values for other hashes, on the way.
$DeltaMEq = $EFG / 45; # 45 meridian spacings along equator for half an octant
$DeltaX5 = 5 * $DeltaFrigid;
foreach $m (0 .. 45) { # Loop for each meridian.
$M = $m . ',' ; # part of hash key (array row number)
# Assign Frigid distance of parallels per degree of latitude.
$dP {$M . 0} = $DeltaFrigid;
# Start point of meridians
if ($m % 5 == 0) { # Every fifth meridian starts at A
$xJ {$M . 0} = $xA; $yJ {$M . 0} = $yA;
} else { # Minor meridians start at 85° lat, that is 5° from A
$xJ {$M . 0} = $xA + $DeltaX5 * cos (deg2rad($m));
$yJ {$M . 0} = $yA + $DeltaX5 * sin (deg2rad($m));
}
# End point of meridians, that is, equidistant intersections with equator;
# These are also the meridian crossings for the zero-th parallel
$distance = $m * $DeltaMEq;
if ($distance <= $yF) {
$xJ {$M . 3} = $xP {$M . 0} = $xG;
$yJ {$M . 3} = $yP {$M . 0} = $distance;
} else { # Past joint at point F
$extra = $distance - $yF;
$xJ {$M . 3} = $xP {$M . 0} = Interpolate ($extra, $EF, $xF, $xE);
$yJ {$M . 3} = $yP {$M . 0} = Interpolate ($extra, $EF, $yF, $yE);
}
# Calculate both joints of meridians
if ($m == 0) { # Straight meridian at center of octant
# This is a good place to calculate a bunch of things for center line, AG.
# No joints; give coordinates of point G for the joints
@xJ {$M . 1, $M . 2} = ($xG, $xG);
@yJ {$M . 1, $M . 2} = ($yG, $yG);
# Length of meridian segments; this whole meridian is a single segment
@L {$M . 0, $M . 1, $M . 2, $M . 3, $M . 4} = ($AG, 0, 0, $AG, $AG);
# May as well calculate parallel intersections along this straight line
foreach $p (75 .. 89) { # (foreach doesn't like first value greater than last)
$xP {$M . $p} = $xA + (90 - $p) * $DeltaFrigid;
$yP {$M . $p} = $yA;
}
# Remaining parallels are equidistant over remaining meridian length
$delta = ($xG - $xP {$M . 75}) / 75;
foreach $p (1 .. 74) { # Parallel 0° was done with end point of meridians
$xP {$M . $p} = $xG - ($p * $delta);
$yP {$M . $p} = $yG;
}
# Distance between parallels
@dP {$M . 1, $M . 2, $M . 3} = ($delta, $delta, $delta);
@L {$M . 5} = $AG - $xP {$M . 73};
} else { # Meridians other than 0°.
# Calculate joints by line intersection from A and M
($flag, $xJ {$M . 1}, $yJ {$M . 1}) =
LineIntersection ($xM, $yM, 2*$m/3, $xA, $yA, $m);
if ($flag ne "Intersect") { die "$flag while calculating 1st joint at $m.\n"; }
($flag, $xJ {$M . 2}, $yJ {$M . 2}) =
LineIntersection ($xM, $yM, 2*$m/3, $xJ {$M . 3}, $yJ {$M . 3}, $m/3);
if ($flag ne "Intersect") { die "$flag while calculating 2st joint at $m.\n"; }
# Calculate length of meridian segments: These are calculated from point A
# to equator, even if this meridian starts at parallel 85°.
$L {$M . 0} = Length ($xA, $yA, $xJ {$M . 1}, $yJ {$M . 1});
$L {$M . 1} = Length ($xJ {$M . 1}, $yJ {$M . 1}, $xJ {$M . 2}, $yJ {$M . 2});
$L {$M . 2} = Length ($xJ {$M . 2}, $yJ {$M . 2}, $xJ {$M . 3}, $yJ {$M . 3});
$L {$M . 3} = $L {$M . 1} + $L {$M . 2}; # Torrid + Temperate
$L {$M . 4} = $L {$M . 3} + $L {$M . 0}; # Total meridian length from A
} # End of calculating meridian joints
} # End of loop for each meridian.
# Do each parallel.
# Do parallels for Frigid region: Parallel 75° to 89°
foreach $p (75 .. 89) {
foreach $m (1 .. 45) {
$M = $m . ',' ;
$distance = (90 - $p) * $dP {$M . 0}; # $dP {$M . 0} = $DeltaFrigid
$xP {$M . $p} = Interpolate ($distance, $L {$M . 0}, $xA, $xJ {$M . 1});
$yP {$M . $p} = Interpolate ($distance, $L {$M . 0}, $yA, $yJ {$M . 1});
}
} # End of Frigid region parallels
# Do supple zone: Parallels 73° and 74°
$distance75 = (90 - 75) * $DeltaFrigid; # Distance from pole to parallel 75
foreach $p (73 .. 74) { # Do only up to meridian 30°; rest is supple zone
foreach $m (1 .. 30) {
$M = $m . ',' ;
# For these meridians, the "supple zone" parallel distance is the same as
# for meridian 0°, since these parallels are circular arcs for this stretch.
$dP {$M . 1} = $dP {0 . ',' . 1};
$distance = $distance75 + (75 - $p) * $dP {$M . 1};
$xP {$M . $p} = Interpolate ($distance, $L {$M . 0}, $xA, $xJ {$M . 1});
$yP {$M . $p} = Interpolate ($distance, $L {$M . 0}, $yA, $yJ {$M . 1});
if ($p == 73) {
$L {$M . 5} = $L {$M . 4} - $distance; # Distance 0° to 73°
}
}
}
# Find intersection meridian 45° with parallel 73°, by a straight line from meridian 30°,
# perpendicular to line BD (or MN). Then calculate supple distances and rest of parallels
# 73° and 74°
$M = 45 . ',' ;
($flag, $xP {$M . 73}, $yP {$M . 73} ) =
LineIntersection ($xP {30 . ',' . 73}, $yP {30 . ',' . 73}, -60, $xB, $yB, 30);
if ($flag ne "Intersect") { die "$flag while calculating 45,73.\n"; }
# Supple zone parallel distance is half of parallel 73° to 75°; at meridian 45°, it goes over
# a joint at point B.
$L {$M . 5} = $L {$M . 4} - Length ($xP {$M . 73}, $yP {$M . 73}, $xB, $yB) - $AB;
$dP {$M . 1} = ( Length ($xP {$M . 73}, $yP {$M . 73}, $xB, $yB) +
Length ($xB, $yB, $xP {$M . 75}, $yP {$M . 75}) ) / 2;
$xP {$M . 74} = Interpolate ( ($distance75 + $dP {$M . 1}), $AB, $xA, $xB);
$yP {$M . 74} = Interpolate ( ($distance75 + $dP {$M . 1}), $AB, $yA, $yB);
foreach $m (31 .. 44) {
$M = $m . ',' ;
# Intersect meridian with straight parallel line from meridian 30° (to 45°)
($flag, $xP {$M . 73}, $yP {$M . 73}) =
LineIntersection ($xP {30 . ',' . 73}, $yP {30 . ',' . 73}, -60, $xA, $yA, $m);
if ($flag ne "Intersect") { die "$flag while calculating $m,73.\n"; }
$L {$M . 5} = $L {$M . 4} - Length ($xP {$M . 73}, $yP {$M . 73}, $xA, $yA);
# Supple zone parallel distance is half of parallel 73° to 75°; at these meridians it
# does not go over a meridian joint; this only happens on meridian 45° (or some
# meridians greater than 44°, if we did them for less than 1° interval).
$dP {$M . 1} = Length($xP {$M.73}, $yP {$M.73}, $xP {$M.75}, $yP {$M.75}) / 2;
$xP {$M . 74} = Interpolate (($distance75+$dP{$M.1}), $L{$M.0}, $xA, $xJ {$M.1});
$yP {$M . 74} = Interpolate (($distance75+$dP{$M.1}), $L{$M.0}, $yA, $yJ {$M.1});
}
# Calculate parallel crossings from 1° to 72° of latitude, for meridians 1° to 29°, plus 45°;
# meridians 30° to 44° are dealt with separately.
foreach $m (1 .. 29) {
$M = $m . ',' ;
# For these meridians, the distance between parallels is the same for both the
# Temperate and Torrid zones, and is 1 / 73 [for parallels 0° to 73°] of
# (total length - distance pole to parallel 75° - twice the supple area parallel
# distance) [twice the supple zone is for parallel 75° to 73°].
# In other words, 1 / 73 of distance from equator to parallel 73°, along meridian line.
$dP {$M . 2} = $dP {$M . 3} = ($L {$M . 4} - $distance75 - 2 * $dP {$M . 1}) / 73;
foreach $p (1 .. 72) {
$distance = $p * $dP {$M . 2};
if ($distance <= $L {$M . 2} ) { # Torrid segment
$xP{$M.$p} = Interpolate ($distance, $L{$M.2}, $xJ{$M.3}, $xJ{$M.2});
$yP{$M.$p} = Interpolate ($distance, $L{$M.2}, $yJ{$M.3}, $yJ{$M.2});
} elsif ($distance <= $L {$M . 3} ) { # Temperate segment, past one joint
$extra = $distance - $L {$M . 2};
$xP{$M.$p} = Interpolate ($extra, $L{$M.1}, $xJ{$M.2}, $xJ{$M.1});
$yP{$M.$p} = Interpolate ($extra, $L{$M.1}, $yJ{$M.2}, $yJ{$M.1});
} else { # Frigid segment, past two joints
$extra = $distance - $L {$M . 3};
$xP{$M.$p} = Interpolate ($extra, $L{$M.0}, $xJ{$M.1}, $xA);
$yP{$M.$p} = Interpolate ($extra, $L{$M.0}, $yJ{$M.1}, $yA);
}
} # End of foreach $p loop
} # End of parallels from latitude 1° to 72°, between meridians 1° and 29°
# Calculate parallel crossings at meridian 45°: point D is parallel 15°; parallels are equally
# spaced from 0° to 15° latitude, and also equally spaced from 15° to 73° latitude.
$M = 45 . ',' ;
$xP {$M . 15} = $xD; $yP {$M . 15} = $yD;
$dP {$M . 2} = Length ($xD, $yD, $xP {$M . 73}, $yP {$M . 73} ) / (73 - 15);
$dP {$M . 3} = $EF / 15; # $EF = length E to F = length E to D
foreach $p (1 .. 15) {
$distance = $p * $dP {$M . 3};
$xP {$M . $p} = Interpolate ($distance, $EF, $xE, $xD);
$yP {$M . $p} = Interpolate ($distance, $EF, $yE, $yD);
}
foreach $p (16 .. 72) {
$distance = ($p - 15) * $dP {$M . 2};
$xP {$M . $p} = Interpolate ($distance, $L {$M . 1},$xD, $xB);
$yP {$M . $p} = Interpolate ($distance, $L {$M . 1},$yD, $yB);
}
# Parallel 15°, and parallels 1° to 72°, between meridians 29° and 45°.
# Parallel 15° is a circular arc from meridian 29° to meridian 45°; center of circle on x-axis.
$P = ',15';
# Find center of chord for parallel 15°, between meridians 29° and 45°
$xmid = ($xP{29 . $P} + $xP{45 . $P}) / 2;
$ymid = ($yP{29 . $P} + $yP{45 . $P}) / 2;
# Slope of this chord is delta-y/delta-x; slope of perpendicular line is -delta-x/delta-y
$mmid = - ($xP{29 . $P} - $xP{45 . $P}) / ($yP{29 . $P} - $yP{45 . $P});
$midAngle=rad2deg(atan($mmid));
# Choose center to be point at intersection of this line with side of octant (that is, side
# which has angle 30° and corresponds to meridian 45°). [ ($xM,$yM) = (0,0) ]
($flag,$xC,$yC) = LineIntersection ($xM,$yM,30,$xmid,$ymid,$midAngle);
if ($flag ne "Intersect") { die "$flag while calculating center of circle for P 15°.\n"; }
$R = Length($xC,$yC,$xP{29 . $P},$yP{29 . $P}); # Radius of circle
$R2 = Length($xC,$yC,$xP{45 . $P},$yP{45 . $P}); # Radius for comparison; checks
print "Chord has ends at ",$xP{29 . $P},",",$yP{29 . $P}," and ",$xP{45 . $P}, ",";
print $yP{45 . $P},"\nMid-point of chord is at $xmid,$ymid;\n";
print "Center of circle is at $xC,$yC;\n";
print "Slope of ray through mid-point is $mmid and corresponding angle is $midAngle.\n";
print "Radius of circular arc is $R or $R2.\n";
# Do all the calculations of intersections of parallels with meridians 30° to 44°
foreach $m (30 .. 44) {
$M = $m . ',';
# Find intersection of circle with meridian; try torrid segment first
($flag,$xP{$m.$P},$yP{$m.$P}) = CircleLineIntersection($xC,$yC,$R,
$xJ{$M . 3},$yJ{$M . 3},$xJ{$M . 2},$yJ{$M . 2});
if ($flag==1) { # found an intersection point
# Distance Equator to parallel 15°.
# warn "Parallel 15° at meridian $m is in torrid zone.\n";
$dist15 = Length ($xP{$m.$P},$yP{$m.$P},$xJ{$M . 3},$yJ{$M . 3});
$dP{$M . 3} = $dist15 / 15;
$dP{$M . 2} = ($L{$M . 5} - $dist15) / 58;
} else { # intersection is on temperate segment
($flag,$xP{$m.$P},$yP{$m.$P}) = CircleLineIntersection($xC,$yC,$R,
$xJ{$M . 2},$yJ{$M . 2},$xJ{$M . 1},$yJ{$M . 1});
if ($flag==0) { # Hmmm.... no intersection!
print "No line-circular arc intersection for M $m, at parallel 15!";
die;
}
# Distance Equator to parallel 15°.
$dist15=Length($xP{$m.$P},$yP{$m.$P},$xJ{$M. 2},$yJ{$M. 2})+$L{$M. 2};
$dP{$M . 3} = $dist15 / 15;
$dP{$M . 2} = ($L{$M . 5} - $dist15) / 58;
}
# Calculate parallel crossings for latitudes 1° to 14°.
# Note that there might be a joint below parallel 15°.
foreach $p (1 .. 15) {
$distance = $p * $dP {$M . 3};
if ($distance <= $L {$M . 2} ) { # Torrid segment
$xP{$M.$p} = Interpolate ($distance, $L{$M.2}, $xJ{$M.3}, $xJ{$M.2});
$yP{$M.$p} = Interpolate ($distance, $L{$M.2}, $yJ{$M.3}, $yJ{$M.2});
} else { # Temperate segment, past one joint
$extra = $distance - $L {$M . 2};
$xP{$M.$p} = Interpolate ($extra, $L{$M.1}, $xJ{$M.2}, $xJ{$M.1});
$yP{$M.$p} = Interpolate ($extra, $L{$M.1}, $yJ{$M.2}, $yJ{$M.1});
}
} # End of foreach $p loop for parallels from latitude 1° to 15°
# Calculate parallel crossings for latitudes 16° to 72°, from meridian 30° to 44°;
# they may or may not all be above Tropical joint on the meridian.
foreach $p (16 .. 72) {
$distance = ($p - 15) * $dP {$M . 2} + $dist15; # Distance from Equator
if ($distance <= $L {$M . 2} ) { # Torrid segment
$xP{$M.$p} = Interpolate ($distance, $L{$M.2}, $xJ{$M.3}, $xJ{$M.2});
$yP{$M.$p} = Interpolate ($distance, $L{$M.2}, $yJ{$M.3}, $yJ{$M.2});
} elsif ($distance <= $L {$M . 3} ) { # Temperate segment, past one joint
$extra = $distance - $L {$M . 2};
$xP{$M.$p} = Interpolate ($extra, $L{$M.1}, $xJ{$M.2}, $xJ{$M.1});
$yP{$M.$p} = Interpolate ($extra, $L{$M.1}, $yJ{$M.2}, $yJ{$M.1});
} else { # Frigid segment, past two joints
$extra = $distance - $L {$M . 3};
$xP{$M.$p} = Interpolate ($extra, $L{$M.0}, $xJ{$M.1}, $xA);
$yP{$M.$p} = Interpolate ($extra, $L{$M.0}, $yJ{$M.1}, $yA);
}
} # End of foreach $p loop for parallels 16° to 72°
} # End of parallels from latitude 1° to 72°, at meridians 30° and 44°
# Output all the values in spreadsheet readable csv format (actually, it is tab separated
# format instead of comma separated format).
open (CSV, ">Macros8\/Hashes8.csv") ||
die "Sorry, I couldn\'t create " . ">Macros8\/Hashes8.csv" . "\n ";
print CSV "\ndP\n"; PrintHash (3,%dP);
print CSV "\nL\n"; PrintHash (5,%L);
print CSV "\nxJ\n"; PrintHash (3,%xJ);
print CSV "\nyJ\n"; PrintHash (3,%yJ);
print CSV "\nxP\n"; PrintHash (89,%xP);
print CSV "\nyP\n"; PrintHash (89,%yP);
# Print coordinates of points of half-octant and scaffold triangle
print CSV "\nPoints";
foreach $i qw(A B D E F G M N Center) {printf CSV "\t%s",$i; }
print CSV "\nx";
foreach $i ($xA,$xB,$xD,$xE,$xF,$xG,$xM,$xN,$xC) {printf CSV "\t%11.4f", $i};
print CSV "\ny";
foreach $i ($yA,$yB,$yD,$yE,$yF,$yG,$yM,$yN,$yC) {printf CSV "\t%11.4f", $i};
# Print lengths of line segments of half-octant and scaffold triangle
print CSV "\n\nLengths";
foreach $i qw(AB BD DE EF FG AG MG MN GN MA MB EFG ABDE R)
{printf CSV "\t%s",$i; }
print CSV "\n";
# length DE = length AB = length EF; also, length GN = y of point N
foreach $i ($AB,$BD,$EF,$EF,$FG,$AG,$xG,$MN,$yN,$MA,$MB,$EFG,2*$EFG,$R)
{printf CSV "\t%11.4f", $i}; print CSV "\n";
close (CSV);
print 'Wrote values of arrays to file "Macros8/Hashes8.csv".', "\n";
# - - - - - - - - - SUBROUTINES - - - - - - - - - - - - -
sub PrintHash {
# Prints one of my two-dimension arrays in the form of a hash; it is assumed that
# the indexes are separated by a comma, the first index varies from 0 to 45 and the
# second index varies from 0 to the first input parameter.
# Values are printed to filehandle CSV.
my ($nI, %Hash) = @_;
my ($i,$m);
foreach $i (0 .. 45) { printf CSV "\t%10d",$i; } print CSV "\n";
foreach $i (0 .. $nI) {
print CSV $i;
foreach $m (0 .. 45) {
if (defined ($Hash{$m.",".$i})) {printf CSV "\t%11.4f",$Hash{$m.",".$i};
} else { printf CSV "\t undef"; }
}
print CSV "\n";
}
} # End of sub PrintHash
sub LineIntersection { # Written 2010-02-28
# Subroutine/function to calculate coordinates of point of intersection of two lines which
# are given by a point on the line and the line's slope angle in degrees.
#
# Return is an array of either one or three values:
# - if the lines don't intersect or are the same, the return is "Parallel";
# - if the lines intersect, the returns are: "Intersect" to mean that it worked, and
# the x and y coordinates of the point of intersection.
# - if not enough arguments were given or the angles were too large, then return is
# "Error".
#
# Arguments should be 6, in this order:
# x and y coordinates of point of first line; slope of first line in degrees;
# x and y coordinates of point of second line; slope of second line in degrees;
#
# Equations used are from: slope of line = tangent angle = delta-y / delta-x, and the fact
# that intersection point x,y is on both lines.
use Math::Trig;
my ($nArguments,$xp,$yp,$m1,$m2);
$nArguments=@_ ;
my ($x1,$y1,$angle1,$x2,$y2,$angle2) = @_ ;
if ($nArguments != 6) { # Not the exact number of arguments
print "Sub LineIntersection requires 6 arguments but received $nArguments \n";
return "Error";
} elsif ($angle1<-180 || $angle2<-180 || $angle1>180 || $angle2>180) { # Angles too large
print "Sub LineIntersection: Angles should be between -180 and 180. \n";
return "Error";
} elsif ($angle1==$angle2 || $angle1 == ($angle2+180) || $angle1 == ($angle2-180) ) {
return "Parallel"; # Lines are either parallel or the same line
} elsif ( not defined($x1) || not defined($y1) || not defined($angle1) ||
not defined($x2) || not defined($y2) || not defined($angle2) ) {
print ("Undefined in LineInterpolation: $x1,$y1,$angle1,$x2,$y2,$angle2\n");
return "Error";
} else { # Lines intersect. Calculate point of intersection.
if ($angle1 == 0 || $angle1 == 180 || $angle1 == -180) { # Line 1 horizontal
if ($angle2 == 90 || $angle2 == -90) { # Line 1 horizontal, line 2 vertical
return ("Intersect",$y1,$x2);
} else { # Line 1 horizontal, line 2 slanted
$xp = $x2 - ($y2 - $y1) / tan(deg2rad($angle2));
return ("Intersect",$xp,$y1);
}
} elsif ($angle1 == 90 || $angle1 == -90) { # Calculate when line 1 is vertical
if ($angle2 == 0 || $angle2 == 180 || $angle2 == -180) {
# Line 1 vertical, line 2 horizontal
return ("Intersect",$x1,$y2);
} else { # Line 1 vertical, line 2 slanted
$yp = $y2 - ($x2 - $x1) * tan(deg2rad($angle2));
return ("Intersect",$x1,$yp);
}
} elsif ($angle2 == 0 || $angle2 == 180 || $angle2 == -180) {
# Line 1 slanted, line 2 horizontal
$xp = $x1 - ($y1 - $y2) / tan(deg2rad($angle1));
return ("Intersect",$xp,$y2);
} elsif ($angle2 == 90 or $angle2 == -90) { # Line 1 slanted, line 2 vertical
$yp = $y1 - ($x1-$x2) * tan(deg2rad($angle1));
return ("Intersect",$x2,$yp);
} else { # Line 1 slanted, line 2 slanted
$m1 = tan(deg2rad($angle1));
$m2 = tan(deg2rad($angle2));
$xp = ($m1 * $x1 - $m2 * $x2 - $y1 + $y2) / ($m1 - $m2);
$yp = $m1 * $xp - $m1 * $x1 + $y1;
return ("Intersect",$xp,$yp);
} #End of all the vertical, horizontal, slanted combinations
} # End of if-else — lines intersect
} # End of sub LineIntersection
sub Length {
# Input are x1,y1,x2,y2
my ($x1,$y1,$x2,$y2) = @_;
return sqrt( ($x1-$x2)**2 + ($y1-$y2)**2);
} # End of sub Length
sub Interpolate {
# Inputs are 4: length wanted, of total-segment-length, start, end;
# Total-segment-length is different from (end - start); end and start may be x-coordinates,
# or y-coordinates, while length takes into account the other coordinates.
# (Start - End ) / Length = (Wanted - Start) / NewLength
# Returns single value: Wanted.
my ($NewLength, $Length, $Start, $End) = @_;
my ($Wanted);
$Wanted = $Start + ($End - $Start) * $NewLength / $Length;
return $Wanted;
} # End of sub Interpolate
sub CircleLineIntersection {
# Subroutine to calculate intersection of circle with line segment. Equations from
# http://local.wasp.uwa.edu.au/~pbourke/geometry/sphereline/
# Arguments are 7, in the following order:
# Circle given as x-center, y-center, radius; line segment given as (x1,y1), (x2,y2).
# If line segment does not intersect circle, return is 0; else, return is 1,x,y of
# point of intersection; it is assumed that circle only intersects line segment at one
# point. If you want a subroutine for other purposes, read that website.
my ($n);
$n = @_;
if ( $n != 7) {
print "Sub CircleLineIntersection requires 7 arguments but got $n.\n";
return 0;
}
my ($xc,$yc,$r,$x1,$y1,$x2,$y2) = @_;
my ($u1,$u2,$a,$b,$c,$d,$x,$y);
# Check if there is a point of intersection
$a = ($x2-$x1)**2 + ($y2-$y1)**2;
$b = 2 * ( ($x2-$x1) * ($x1-$xc) + ($y2-$y1) * ($y1-$yc) );
$c = $xc**2 + $yc**2 + $x1**2 + $y1**2 - 2 * ($xc*$x1 + $yc*$y1) - $r**2;
$d = $b**2 - 4*$a*$c; # Determinant
if ($a == 0) {
# print "In sub CircleLineIntersection: line given is just one point!\n";
return 0;
}elsif ($d < 0) {
# Determinant is negative: circle does not intersect the line, much less the
# segment
# print "In sub CircleLineIntersection: line doesn't intersect circle.\n";
return 0;
}
# $u1 and $u2 are the roots to a quadratic equation
$u1 = (-$b + sqrt($d) ) / (2*$a); # + of +/- of the solution to the quadratic equation
$u2 = (-$b - sqrt($d) ) / (2*$a); # - of +/- of the solution to the quadratic equation
# Check if there is an intersection and if it is within the line segment (not only the line)
# If $u1=$u2, line is tangent to the circle; if $u1 != $u2, line intersects circle at two
# points; however, point or points of intersection are within the line segment only if
# the root is within interval [0,1].
if (0 <= $u1 && $u1 <= 1) { # This root is on the line segment; use it
$x = $x1 + $u1 * ($x2 - $x1);
$y = $y1 + $u1 * ($y2 - $y1);
return 1,$x,$y;
} elsif (0 <= $u2 && $u2 <= 1) {
# 1st root was not on line segment but 2nd one is; use it
$x = $x1 + $u2 * ($x2 - $x1);
$y = $y1 + $u2 * ($y2 - $y1);
return 1,$x,$y;
} else { # neither root is on line segment
# print "In sub CircleLineIntersection: line segment doesn't intersect circle.\n";
return 0;
}
} # End of sub CircleLineIntersection