From Geografiska Annaler, Vol.
16, 1934, p. 97-108
Digitized and reformatted in HTML by Gene Keyes, 2009-03-18
Digitized and reformatted in HTML by Gene Keyes, 2009-03-18
97
>>
A WORLD MAP TO END WORLD MAPS >>
by B. J. S. CAHILL, ALAMEDA,
CALIFORNIA U. S. A.
>>On a
practical issue men wish to reach a conclusion.>>
Bertrand Russell.
Bertrand Russell.
A very practical issue of our day is
the problem of adequately mapping the World on a single
sheet. This problem has too often been considered merely
as an extension of those principles employed in
projecting regional or national maps. This has led to
confusion of thought because the two operations are
different in kind; not in degree. Each calls for a
separate approach. Strictly mathematical methods will
suffice in mapping any part of the globe, but not in
mapping the whole of it. The latter problem demands
deliberate design of the creative or intuitional rather
than the analytical type of mind. Since things which
resemble the same thing resemble one another it follows
that the closer the portraiture the smaller the range of
variation. When finally map and globe practically agree,
there can no longer be any substantial variation, and
the need of further world mapping comes naturally to an
end.
While the logic of this seems indisputable, the geodesists keep on inventing different projections and telling us that their possible number is »an infinity of infinities»: which means that »contributions» to the subject will keep accumulating until doomsday. But, in the nature of things, there must be one system of world mapping better than any other. This system, which the author set out a generation ago to discover is now briefly described in the following pages.
So far we have spoken of mapping the world with the implication that a map expresses »portraiture» while specific »purpose» is expressed by the world chart. Moreover, in a chart, the sea is usually the more important, in a map, the land.
With one exception, to be noted later on, we are not concerned with charts which are not also maps, nor with isolated regions. Projections for these have been exhaustively developed and perfected by many of the world's most eminent mathematicians and they represent by far the largest part of the science of projection. No claim whatever is made as to any development or improvement here. On the contrary, the principles established in these maps are accepted bodily and. applied later in the details and subordinate parts of the general design or holding frame; the displayed faces of a regular globe enveloping octahedron. Thus, while the Butterfly Map or Octahedral system of projection brings nothing new to the mathematics of the subject, it limits and controls the various methods in use to the end that the form and features of mother earth shall be as faithfully portrayed as possible. It is primarily a problem of design to the solution of which the training and practice of an architect is perhaps as good, if not a better qualification than that of a geodesist.
98 B.J.S. Cahill
»The Architect», to quote Professor
Leighly, geographer, of the University of California, »is
accustomed to the transformation of three-dimensional
bodies into plane figures. This ability to manipulate
geometric figures in space, which becomes second nature to
him, may well be envied by anyone who deals with maps. The
relatively sterile concepts of. the mathematician in this
field are rendered fruitful only by this plastic
imagination which the architect cultivates to the highest
degree».
A map is a plan and in many
lands the architect is also a surveyor. He is familiar
with problems of scale and all his drawings are
projections. He is a master of diagram, symmetry and
form. But far more important is his severe training in
problems of compromise. In any great structure there are
innumerable conflicting demands all seemingly imperative
yet none of which can be fully met without sacrificing
others. Yet they must all be duly considered, adjusted
and finally welded in a balanced product, the perfect
plan.
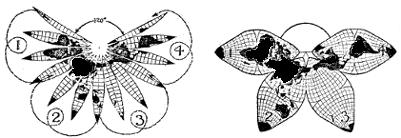
Fig.1. The common sense origin
of the Butterfly Map.
The gores of a globe assembled where the major land masses naturally cohere, not at the Pole nor at the Equator, but at the. North Temperate Zone with the radiating extensions of land plateaux and archipelagoes gathered into four Southern lobes, later divided into eight parts or octants.
This is precisely the problem of making a eumorphic world map. By no miracle can the surface of half, much less the whole of a sphere be laid out flat in a square, a disc or an ellipse without excessive exaggeration or distortion. Yet a working compromise must be arrived at. How? By first realizing that we are to devise a land map of portraiture and not a sea chart of purpose. Then to bring the. problem within the easy grasp of everyone it is only necessary to conceive the continents as a limited land pattern on the much larger water surface of the globe which must be symmetrically cut out so that it can be uniformly laid flat. Or, conversely, we must design an orderly world pattern on a piece of fabric, the containing seas, so outlined that it can be fitted around a sphere with a minimum of stretching.
From this it is at once quite clear that no rectangular, circular or elliptical piece of cloth can be fitted round a ball or even half of one. And from this it further follows that no world map nor hemisphere plotted within such boundaries can
>>A World Map to End World Maps>> 99
[Ed. note: for a double-size, horizontal image in a new window, click here. My online version is better than the original! — GK]
100 B.J.S. Cahill
possibly possess the degree of
eumorphism or general atlas accuracy which we are seeking.
It is also necessary to design the shape of our piece of fabric in such a way that it will (1) fit around the sphere itself or a closely enveloping regular solid and also (2) be so divided that the inner mathematical weave shall in no portion be stretched beyond a reasonable definite limit.
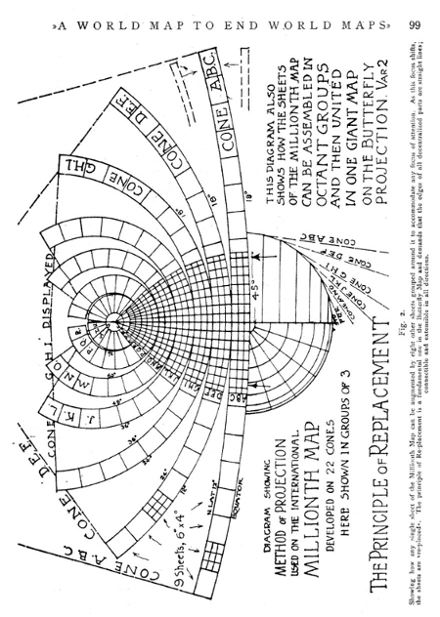
By cutting our fabric in vertical fusiform. gores, or into very many small facets we can achieve our end as in the case of a geographical globe or the International Millionth map, neither of which can be completely assembled on any but spherical surfaces.
But we have to show the continental pattern laid flat on a plane without disruption of the land masses as on the gores of a globe, and in much larger cohering units than the .2,000 odd sheets of the Millionth map, even when any nine of them are assembled into one.
The plan finally adopted however, retains something of the character of both these methods.
First we group the gores in eight bundles of six instead of the forty-eight pasted on a globe. Then we show the whole of the world in eight separate parts instead of grouping eight sheets around any one of the so-called Millionth »map» (a misnomer), to form a cohering unit. In both instances we obtain a continuum by successive replacement.
On the Butterfly map any octant sheet can be a starting place for the eight which comprise the earth, whereas on the Millionth map, any sheet can be augmented by the eight surrounding it. Both systems display a new principle in world mapping: the mechanical replacement of parts which are constant to accommodate a focus of attention which is variable.
It took much time and thought to arrive at the octahedral frame. It is made by the intersection of three planes at right angles to one another passing through the center of the earth and dividing the surface into eight curvilinear equilateral triangles, contained in the displayed facets of. a regular enveloping octahedron.
Thus by limiting the scope of the projected surface to one eighth of the earth's area, excessive marginal distortion is impossible. Moreover, as in this limited area the central focus of accuracy broadens out, the region of cumulative error grows narrower toward the corners, until, when at the maximum of its exaggeration, it is also at the minimum of its extent.
It took many more years of study provoked by criticism and comment before the intensive details were developed definitely and before the final evolution of the three variants, within the decentralized octahedral frame.
Nor, as we said at the outset, can
any extension from one point; arc or line be continued
indefinitely without excessive enlargement at the edges.
Decentralization therefore is imperative.
It is also necessary to design the shape of our piece of fabric in such a way that it will (1) fit around the sphere itself or a closely enveloping regular solid and also (2) be so divided that the inner mathematical weave shall in no portion be stretched beyond a reasonable definite limit.
By cutting our fabric in vertical fusiform. gores, or into very many small facets we can achieve our end as in the case of a geographical globe or the International Millionth map, neither of which can be completely assembled on any but spherical surfaces.
But we have to show the continental pattern laid flat on a plane without disruption of the land masses as on the gores of a globe, and in much larger cohering units than the .2,000 odd sheets of the Millionth map, even when any nine of them are assembled into one.
The plan finally adopted however, retains something of the character of both these methods.
First we group the gores in eight bundles of six instead of the forty-eight pasted on a globe. Then we show the whole of the world in eight separate parts instead of grouping eight sheets around any one of the so-called Millionth »map» (a misnomer), to form a cohering unit. In both instances we obtain a continuum by successive replacement.
On the Butterfly map any octant sheet can be a starting place for the eight which comprise the earth, whereas on the Millionth map, any sheet can be augmented by the eight surrounding it. Both systems display a new principle in world mapping: the mechanical replacement of parts which are constant to accommodate a focus of attention which is variable.
It took much time and thought to arrive at the octahedral frame. It is made by the intersection of three planes at right angles to one another passing through the center of the earth and dividing the surface into eight curvilinear equilateral triangles, contained in the displayed facets of. a regular enveloping octahedron.
Thus by limiting the scope of the projected surface to one eighth of the earth's area, excessive marginal distortion is impossible. Moreover, as in this limited area the central focus of accuracy broadens out, the region of cumulative error grows narrower toward the corners, until, when at the maximum of its exaggeration, it is also at the minimum of its extent.
It took many more years of study provoked by criticism and comment before the intensive details were developed definitely and before the final evolution of the three variants, within the decentralized octahedral frame.
>>A World Map to End World Maps>> 101
[Ed. note: for a double-size, horizontal image in a new window, click here. Again, my online re-enlargement is more readable than the journal's reduction as shown here. Cahill's versions were 2.5 to 12.8 times larger than the above.
— GK]
102 B.J.S. Cahill
Just as eumorphism is attained by
limiting the scope, so three-way continuity is contrived
by straightening the boundaries.
By this device all studies of problems spreading over random regions can be indefinitely continued from one octant to another. Thus in one world map is combined the general accuracy of an atlas with the continuity of a globe but without the scale variety of the former or the curved surface of the latter.
The accuracy can be proved and the continuity effected by mechanical means, and since the octants are separate units they can be assembled four ways in the butterfly form besides into groups of four showing the eastern and western or the northern and southern hemispheres. Other forms and combinations in great number will readily suggest themselves. For instance, great circle belts 90° wide clear around the world through six octants can be extended from any one octant in three directions, thus yielding in effect three separate pseudo-cylindrical maps each capable of six different positions, all built up from one set of plates differently arranged. In type »C», of the Equivalent Variant great circle belts 45° wide in three more different directions through the corners of each octant can be similarly arranged.
The notion that a World map must be in a compact indivisible form and not in articulated movable parts, is largely a mental habit of thought engendered by long contemplation of .Mercator's chart designed to straighten the rhumb line and later, Mollweide's elliptical monstrosity and its descendants. Those solid formations where vast oceanic spaces are fantastically stretched instead of being frankly cut, are still preferred by many geodesists who are more interested in their mathematics than in the map. As for the replacement of parts, a globe itself must be mechanically moved to be adequately seen: better to rearrange plates than to reengrave them: and very much better to have one conclusive model than many inconclusive ones.
To compute a variety of world map projections is a very laborious and costly task. To engrave and publish them with sufficient detail to be of value is still more so. In fact it seems to the author to be self evident that a diversity of world maps is as serious a drawback to the advancement of international geosophical science as a diversity of time systems and prime meridians would be.
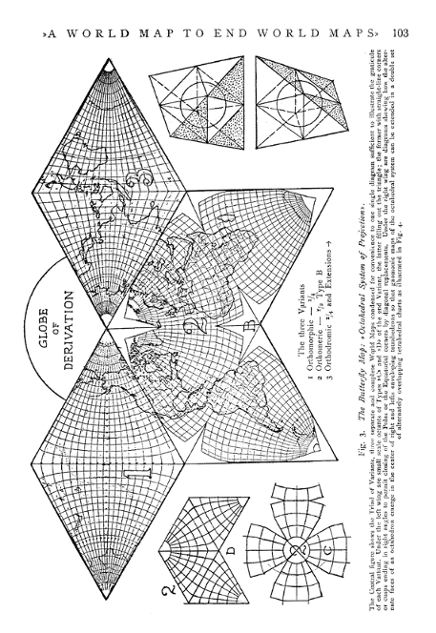
The Three Variants within the decentralized octahedral frame are described as to construction, purpose and application as follows:
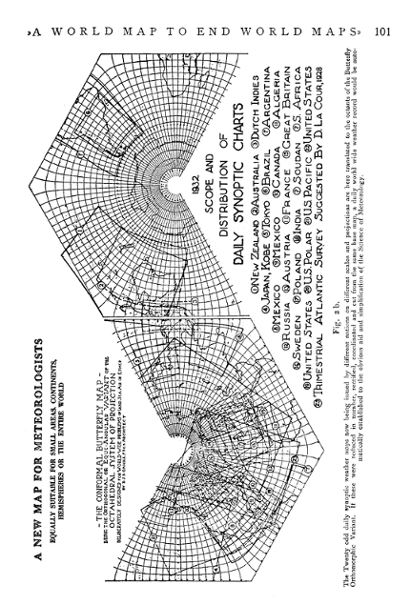
(I). The Conformal, Orthogonal or Orthomophic Variant is of the rhombic type suggested to the author by Charles Peirce's quincuncial projection, also an eight part system. The parallels are interlinkmg ellipses whose common foci move along the octant boundaries, while the meridians are in effect orthographically projected conics.) It is best suited as a meteorological base map from which the world's daily synoptic charts can be cut so that when surcharged with synchronized isometric records, they can be reassembled into a daily world weather map in the interest of long range forecasting. Since the map is azimuthal about every point (save six) it, alone of all types of projection, is one in which »winds may be plotted
By this device all studies of problems spreading over random regions can be indefinitely continued from one octant to another. Thus in one world map is combined the general accuracy of an atlas with the continuity of a globe but without the scale variety of the former or the curved surface of the latter.
The accuracy can be proved and the continuity effected by mechanical means, and since the octants are separate units they can be assembled four ways in the butterfly form besides into groups of four showing the eastern and western or the northern and southern hemispheres. Other forms and combinations in great number will readily suggest themselves. For instance, great circle belts 90° wide clear around the world through six octants can be extended from any one octant in three directions, thus yielding in effect three separate pseudo-cylindrical maps each capable of six different positions, all built up from one set of plates differently arranged. In type »C», of the Equivalent Variant great circle belts 45° wide in three more different directions through the corners of each octant can be similarly arranged.
The notion that a World map must be in a compact indivisible form and not in articulated movable parts, is largely a mental habit of thought engendered by long contemplation of .Mercator's chart designed to straighten the rhumb line and later, Mollweide's elliptical monstrosity and its descendants. Those solid formations where vast oceanic spaces are fantastically stretched instead of being frankly cut, are still preferred by many geodesists who are more interested in their mathematics than in the map. As for the replacement of parts, a globe itself must be mechanically moved to be adequately seen: better to rearrange plates than to reengrave them: and very much better to have one conclusive model than many inconclusive ones.
To compute a variety of world map projections is a very laborious and costly task. To engrave and publish them with sufficient detail to be of value is still more so. In fact it seems to the author to be self evident that a diversity of world maps is as serious a drawback to the advancement of international geosophical science as a diversity of time systems and prime meridians would be.
The Three Variants within the decentralized octahedral frame are described as to construction, purpose and application as follows:
(I). The Conformal, Orthogonal or Orthomophic Variant is of the rhombic type suggested to the author by Charles Peirce's quincuncial projection, also an eight part system. The parallels are interlinkmg ellipses whose common foci move along the octant boundaries, while the meridians are in effect orthographically projected conics.) It is best suited as a meteorological base map from which the world's daily synoptic charts can be cut so that when surcharged with synchronized isometric records, they can be reassembled into a daily world weather map in the interest of long range forecasting. Since the map is azimuthal about every point (save six) it, alone of all types of projection, is one in which »winds may be plotted
>>A World Map to End World Maps>> 103
[Ed. note: for a double-size, horizontal image in a new window, click here. — GK]
104 B.J.S. Cahill
with their true directions.. And, if
further, mathematical operations are to be effected, such
as graphic differentiations or integrations, their
execution could scarcely be thought of if the projection
were not conformal». (Professor V. Bjerknes, Geografiska
Annaler, Vol. II, 1920.) The areas of each 5° x 5°
quadrilateral, moreover, will be printed on the map at
each successive latitude to aid in problems of atmospheric
weight distribution.
(II). The Equivalent, Authalic or Orthomeric Variant here shown is based on Albers' equal area projection with some modifications towards the Poles and Equatorial corners. This type is suitable for anthropogeographical purposes, education, graphic statistics and general problems of transportation and travel.
Unlike the Conformal and Gnomonic Variants, this one serves purely geographical rather than strictly scientific geophysical purposes, and therefore has not quite as rigorous a mathematical foundation — in accordance with Max Eckert's very sensible dictum »Das matbematisch beste Netz ist nicht stets auch das geographisch beste». (Die Kartenprojektion, Geographische Zeitschrift t. XVI 1910, p. 391.)
A strictly mathematical alternative Butterfly Equivalent Variant, based on Albers' and Bonne's projections, has, however been designed, computed, drawn and then discarded. for the excellent reason that »the best mathematical net is not always also the best geographical one». This is termed type »A» Variant and the one here illustrated type »B».
Recently the author has designed a third or type »C» Orthomeric Variant which is centrally zenithal or azimuthal with the corner cusps bounded by straight lines instead of curved ones, all three ending in right angles. This makes it possible to unite the octants at their ends, thus closing the polar and equatorial corners which are »open» in the Conformal and Gnomonic Variants.
A fourth or »D» type Orthomeric Variant is also being developed which fills out the whole triangle and is centrally zenithal or azimuthal like the other two Variants. Its parallels are interlinking ellipses with paraboloid meridians. It is computable, consistent and acceptable to geodesists. It may also have an occasional comparative value in the triad of Variants which is lacking in types A, B and C. When these types are completed and computed they will be permanently established, and the: provisional types »A» and »B» will be discarded.
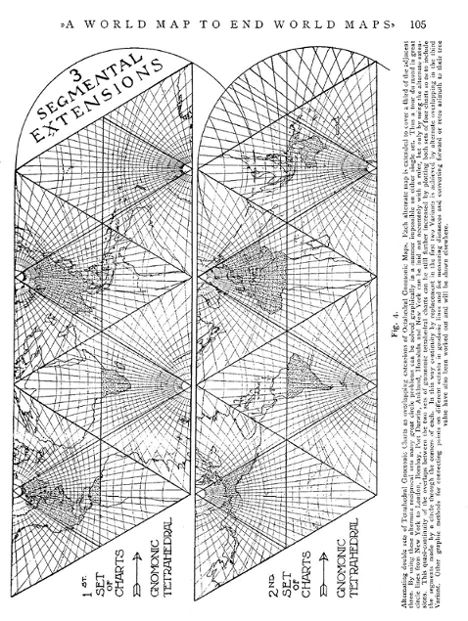
(III). The Gnomonic, Central or Orthodromic Variant consists of eight great circle charts with, however, continuous longitude over each half of the world and continuous latitude over each quarter, all of one graticular pattern and all tangent on latitude 35°-15'-51.8" North or South and longitude 22°-30' East, plus multiples of 90° etc. This variant, together with double tetrahedral extensions is suitable for radio, navigational and geophysical problems of sea, land, air or »ether».
For the first time and because of their eumorphism and quasi-continuous nocharacterted above, it is proposed to give these practically undistorted eight gnomonic charts of the world full topographical details. Alternate sets of four of these are also to be enlarged by encroaching each on one third of the adjacent ones to cover the facets of right and left enveloping tetrahedrons, thus yielding two sets of reccharacter
(II). The Equivalent, Authalic or Orthomeric Variant here shown is based on Albers' equal area projection with some modifications towards the Poles and Equatorial corners. This type is suitable for anthropogeographical purposes, education, graphic statistics and general problems of transportation and travel.
Unlike the Conformal and Gnomonic Variants, this one serves purely geographical rather than strictly scientific geophysical purposes, and therefore has not quite as rigorous a mathematical foundation — in accordance with Max Eckert's very sensible dictum »Das matbematisch beste Netz ist nicht stets auch das geographisch beste». (Die Kartenprojektion, Geographische Zeitschrift t. XVI 1910, p. 391.)
A strictly mathematical alternative Butterfly Equivalent Variant, based on Albers' and Bonne's projections, has, however been designed, computed, drawn and then discarded. for the excellent reason that »the best mathematical net is not always also the best geographical one». This is termed type »A» Variant and the one here illustrated type »B».
Recently the author has designed a third or type »C» Orthomeric Variant which is centrally zenithal or azimuthal with the corner cusps bounded by straight lines instead of curved ones, all three ending in right angles. This makes it possible to unite the octants at their ends, thus closing the polar and equatorial corners which are »open» in the Conformal and Gnomonic Variants.
A fourth or »D» type Orthomeric Variant is also being developed which fills out the whole triangle and is centrally zenithal or azimuthal like the other two Variants. Its parallels are interlinking ellipses with paraboloid meridians. It is computable, consistent and acceptable to geodesists. It may also have an occasional comparative value in the triad of Variants which is lacking in types A, B and C. When these types are completed and computed they will be permanently established, and the: provisional types »A» and »B» will be discarded.
(III). The Gnomonic, Central or Orthodromic Variant consists of eight great circle charts with, however, continuous longitude over each half of the world and continuous latitude over each quarter, all of one graticular pattern and all tangent on latitude 35°-15'-51.8" North or South and longitude 22°-30' East, plus multiples of 90° etc. This variant, together with double tetrahedral extensions is suitable for radio, navigational and geophysical problems of sea, land, air or »ether».
For the first time and because of their eumorphism and quasi-continuous nocharacterted above, it is proposed to give these practically undistorted eight gnomonic charts of the world full topographical details. Alternate sets of four of these are also to be enlarged by encroaching each on one third of the adjacent ones to cover the facets of right and left enveloping tetrahedrons, thus yielding two sets of reccharacter
>>A World Map to End World Maps>> 105
[Ed. note: for a double-size, horizontal image in a new window, click here. — GK]
106 B.J.S. Cahill
procally overlapping expansions of the
original octants, since any octahedron can, by adding
small tetrahedrons to alternate faces, be extended to
positive and negative large tetrahedrons. By means of this
fortunate geometrical fact the orthodromic service of this
double set of tangent planes exceeds by far the service of
any single one possible. Moreover by extending the scope
of each of these tetrahedral triangles to the limits of a
circle through the corners, we have a still further
segmental extension of each overlapping chart embracing
the largest area practically possible on a sheet of
convenient dimensions. These three segmental extensions
will cover the poles for some 15° and also the equatorial
regions to the same extent and include many points and
places of great importance in solving orthodromic problems
by the simple use of a straight-edge or ruler. A detailed
account of this Variant will shortly appear in Petermann's
Mitteilungen.
All the octants of each Variant can be folded so as to connect all edges or bring all eight to the dimensions of one.
All five degree points of intersection in each Variant have been mathematically computed and tabulated in centimeters to three places of decimals, to the scale of 1 : 10 and 1: 14. millions, the latter for the second Variant.
(I). The Orthomorphic Variant develops an elegant mathematical theory in the skillful hands of Dr. Oscar S. Adams (who by the way does not »draw the line at the square root of minus one») and makes a special appeal to the professional geodesist.
(II). The Orthomeric Variant agrees most closely of all with the globe of derivation and will be invariably issued to the scale of a standard globe so that comparisons by calliper can attest its general accuracy. This is moreover a world map in which the element of organic form is most conspicuous. In place of the arabesques, cartouches and ornate framework of the elder cartographers we have an inherent beauty of outline which is functional and not adventitious. The artistic tinting of the land masses in a holding tone of blue-green sea will fit the map for many decorative uses heretofore unheard of, all in the interest of geography and greater public familiarity with the surface features of our planet.
The Butterfly Map is not conceived for the exclusive appraisal of the mathematical virtuoso or geodetic enthusiast, but for the practical use of cartographers and for the furtherance of world study among educated people of all classes in all nations.
(III). The Orthodromic Variant develops new methods for graphic application to a vast number of problems which have only appeared in recent years and which the future needs of geophysical science will multiply manyfold in the years to come. The use of the triangular faces of an octahedron in place of the usual square faces of a cube yields at once better eumorphism than six faces, one pattern to compute instead of two and, in its double extensions to the four planes of a tetrahedron, a scope for charts of purpose on fewer and therefore larger planes than those of a cube or hexahedron.
All the octants of each Variant can be folded so as to connect all edges or bring all eight to the dimensions of one.
All five degree points of intersection in each Variant have been mathematically computed and tabulated in centimeters to three places of decimals, to the scale of 1 : 10 and 1: 14. millions, the latter for the second Variant.
(I). The Orthomorphic Variant develops an elegant mathematical theory in the skillful hands of Dr. Oscar S. Adams (who by the way does not »draw the line at the square root of minus one») and makes a special appeal to the professional geodesist.
(II). The Orthomeric Variant agrees most closely of all with the globe of derivation and will be invariably issued to the scale of a standard globe so that comparisons by calliper can attest its general accuracy. This is moreover a world map in which the element of organic form is most conspicuous. In place of the arabesques, cartouches and ornate framework of the elder cartographers we have an inherent beauty of outline which is functional and not adventitious. The artistic tinting of the land masses in a holding tone of blue-green sea will fit the map for many decorative uses heretofore unheard of, all in the interest of geography and greater public familiarity with the surface features of our planet.
The Butterfly Map is not conceived for the exclusive appraisal of the mathematical virtuoso or geodetic enthusiast, but for the practical use of cartographers and for the furtherance of world study among educated people of all classes in all nations.
(III). The Orthodromic Variant develops new methods for graphic application to a vast number of problems which have only appeared in recent years and which the future needs of geophysical science will multiply manyfold in the years to come. The use of the triangular faces of an octahedron in place of the usual square faces of a cube yields at once better eumorphism than six faces, one pattern to compute instead of two and, in its double extensions to the four planes of a tetrahedron, a scope for charts of purpose on fewer and therefore larger planes than those of a cube or hexahedron.
>>A World Map to End World Maps>> 107
For, after all, it is in the simple
graphic visible uses of a map that its real importance
lies, rather than in the invisible mathematics of its
construction.
The whole design has special reference to the land masses of our particular planet as distinct from a vain attempt to display the surface of an ideal isometric sphere, where all parts are theoretically of equal interest.
In this particular it has a direct international appeal giving invariably the best presentation to the most humanly important regions.
While each Variant preserves its supreme scientific purpose without any taint of compromise or mixture they all present the continents with practical identity of portraiture, so that no nation using the map is favored over another, and the aspect of any region worked over in the interest of one scientific problem is not violently at variance with the same region involved in another.
Thus comparisons of compass directions and great circle lines in studies of terrestrial magnetism and electricity, seismology and isostasy, radio emission and skip distances, etc., would all be simplified on maps of the same size and similar form, in a manner impossible on he wholly dissimilar maps now in general use, where one is conformal and the other gnomonic.
Finally the similarity of the three Variants expressing all the qualities combined in a globe, added to their finality of presentation in a permanent standardized system, makes an irresistible appeal not only to the users of maps, but to the makers of them. With a score of world maps to choose from no publisher would risk the cost on one adequate production while twenty publishers would gladly risk the cost of issuing one system universally agreed upon by all nations for most purposes. This holds also with respect to all government work in meteorological and hydrographic offices, etc.
From the very beginning the author's deliberate aim has been to design a world mapping system, which in the main could not be improved upon and which, sooner or later, would be universally adopted. He is confident that after thirty-five years work he has finally succeeded. Dissent from this view to be effective should indicate another system as good or better. Until that is done the author commits his work to the consideration of his contemporaries and the judgment of posterity.
The whole design has special reference to the land masses of our particular planet as distinct from a vain attempt to display the surface of an ideal isometric sphere, where all parts are theoretically of equal interest.
In this particular it has a direct international appeal giving invariably the best presentation to the most humanly important regions.
While each Variant preserves its supreme scientific purpose without any taint of compromise or mixture they all present the continents with practical identity of portraiture, so that no nation using the map is favored over another, and the aspect of any region worked over in the interest of one scientific problem is not violently at variance with the same region involved in another.
Thus comparisons of compass directions and great circle lines in studies of terrestrial magnetism and electricity, seismology and isostasy, radio emission and skip distances, etc., would all be simplified on maps of the same size and similar form, in a manner impossible on he wholly dissimilar maps now in general use, where one is conformal and the other gnomonic.
Finally the similarity of the three Variants expressing all the qualities combined in a globe, added to their finality of presentation in a permanent standardized system, makes an irresistible appeal not only to the users of maps, but to the makers of them. With a score of world maps to choose from no publisher would risk the cost on one adequate production while twenty publishers would gladly risk the cost of issuing one system universally agreed upon by all nations for most purposes. This holds also with respect to all government work in meteorological and hydrographic offices, etc.
From the very beginning the author's deliberate aim has been to design a world mapping system, which in the main could not be improved upon and which, sooner or later, would be universally adopted. He is confident that after thirty-five years work he has finally succeeded. Dissent from this view to be effective should indicate another system as good or better. Until that is done the author commits his work to the consideration of his contemporaries and the judgment of posterity.
ADDENDUM. Since the above was written, the author has designed another sub-variant, Type »E» of the Orthomeric Butterfly map in which the five Zones can be shown completely by replacements of one Octant diagram. Both poles can be closed in circular discs 45 degrees across. The belts of 45 degrees across the Temperate zones can be shown as in the other variants. In Type »E» the Equator or base of each Octant is a straight line across 90 degrees of longitude with its boundary meridians perpendicular to the Equator 22°.30' North and South, thus
108 B.J.S. Cahill
practically covering the Torrid Zone in
one pseudo-cylindrical horizontal belt indefinitely
continuable either East or West.
See »Static and Climatic World Maps.» a paper read before the American Meteorological Society at the Berkeley, California meeting, June 1934, to be published in the Bulletin of that Society.
See »Static and Climatic World Maps.» a paper read before the American Meteorological Society at the Berkeley, California meeting, June 1934, to be published in the Bulletin of that Society.